下图中的三个绳圈套在一起，没有哪一个绳圈能从中分离出来。不过，真正有趣的是，如果去掉其中任意一个绳圈，那么其他所有的绳圈都全部散开了。如果 n 个绳圈套在一起，并且任意去掉其中一个绳圈都会同时解开其他所有套着的绳圈，我们就把它叫做 n-component Brunnian link 。
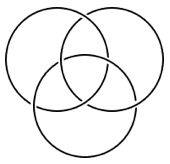
你能想出一个 n = 4 的 Brunnian link 吗？ n = 5 呢？ n 可以任意大吗？
拓扑学
最难的组合游戏：To Knot or Not to Knot
A Midsummer Knot’s Dream 简直可以说是去年学术界的一篇奇文，大家点进去看看就知道了。论文里讲了一个基于纽结理论的双人对弈游戏，名字也非常有艺术感： To Knot or Not to Knot 。这个游戏可能是最难的组合游戏了，它的数学性极强，思考难度非常大，甚至比 ERGO 更不容易上手。一场游戏下来，究竟谁赢谁输可能都不好判断。
To Knot or Not to Knot 的游戏规则非常简单。用铅笔在纸上画一个封闭的、可以自相交的回路，然后 A 、 B 两人轮流在图形中选取一个尚未被处理过的交叉点，并用橡皮擦对图形进行“细化”，明确两根线条的位置关系（可以抛掷硬币决定谁先行动）。A 的目的是要让最终的图形变成一个结，而 B 的目的则是避免图形打结。下面是其中一种可能的游戏过程，双方约定 B 先走。两人轮流对交叉点进行细化，七步之后，整个图形并未打结（你能看出来吗）， B 获得胜利。
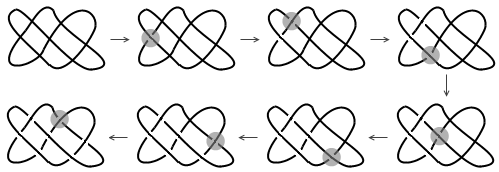
注意，这是一个决策透明、信息公开的游戏，并且游戏不可能有平局产生。因此，即使双方都使出最佳策略，也必然有一个人会赢有一个人会输。也就是说，任意给定一个初始状态，总有一方有必胜的策略。不过，难就难在，究竟谁有必胜策略，必胜策略是什么，这并不容易判断。让我们来做一个练习题吧：下面的图形中，如果 A 先走，B 后走，谁有必胜策略？如果 B 先走，A 后走呢？记住，A 的任务是要让最终的图形打成结，而 B 的任务则是避免图形打结。
趣题：最“悬”的悬挂方式
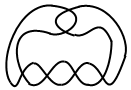
把画框悬挂在钉子上，总是给人一种很不安全的感觉，如果钉子掉了的话，画框也会重重地砸在地上。像上图那样，把画框挂在两颗钉子上，看上去可就安全得多了——如果有一颗钉子掉了的话，画框仍然能够悬挂在另一颗钉子上，就好像上了双保险一样。
今天，我们要考大家一个完全相反的蛋疼问题——如何把画框挂在两颗钉子上，使得去掉任意一颗钉子，画框都会掉下去？
玩转内接多边形（四）：登山引理 一个无关的问题
在继续探索多边形内接图形问题之前，我们先来看一个看似无关的趣题。从水平线上的一点起笔，在这条水平线上方随意画一条折线段，最后回到水平线上（如下图）。把这个折线段想象成一座座山峰。我们以最高峰所在位置为界把整座山分成左右两部分。现在，假设有一对相恋的登山者，一个站在最左侧的山脚出（即点 0 处），一个站在最右侧山脚处（即点 0′ 处）。这两个人将同时从山脚出发，同时到达山顶，并且保证在此过程中他们俩总处于同一海拔高度。不管这座山是什么形状，这种浪漫的想法总可以实现吗？
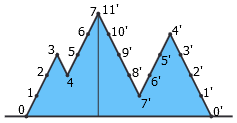
注意，在登山的过程中，登山者可以为了照顾对方而走回头路。例如，对于图中所示的小山，两个人可以按照下列方法实现同步登山。左右两个人的路线分别为：
0 → 1 → 2 → 3 → 4 → 5 → 6 → 5 → 4 → 3 → 2 → 1 → 2 → 3 → 4 → 5 → 6 → 7
0'→ 1'→ 2'→ 3'→ 2'→ 3'→ 4'→ 5'→ 6'→ 5'→ 6'→ 7'→ 8'→ 9'→ 8'→ 9'→ 10'→ 11'
玩转内接多边形（三）：任意凸多边形内均存在内接菱形
当我们进一步考虑内接菱形时，情况有了一些变化——证明任意多边形内均存在内接菱形没有前几个问题那么容易了。但我们可以轻易证明一个弱化版的命题：任意凸多边形内均存在内接菱形。下面将给出这个命题的两种不同的证明，它们都相当经典。
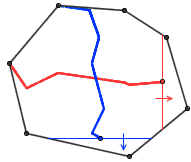
证明 1 ：考虑凸多边形内的一条水平线段由上至下扫过，这条线段的中点所形成的轨迹就是一条连接凸多边形最顶端与最底端的折线段。类似地，考虑一条从左至右移动的竖直线段，它的中点就构成了从凸多边形最左端到最右端的连线。显然，这两条连线会有一个交点，也就是说我们找到了两条互相垂直且中点重合的线段，它们对应的四个端点显然就是一个菱形的四个顶点。