环面多面体,即亏格为 1 的多面体,直观地说就是有 1 个洞的多面体。下图中三个多面体里分别有 0 个洞、1 个洞和 2 个洞。第二个多面体就是环面多面体。最近,我在研究一些和环面多面体相关的话题,在这里和大家分享一些我的发现。
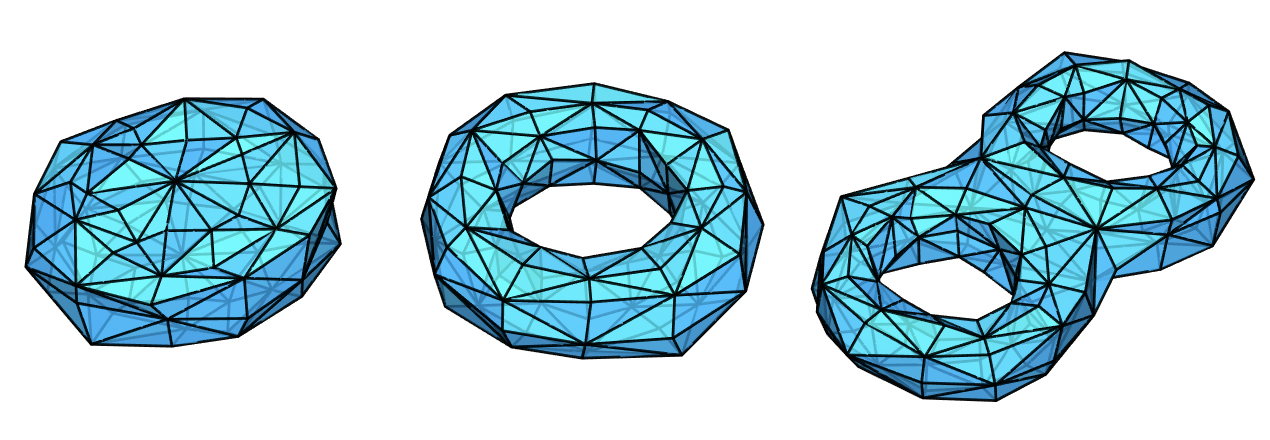
环面多面体,即亏格为 1 的多面体,直观地说就是有 1 个洞的多面体。下图中三个多面体里分别有 0 个洞、1 个洞和 2 个洞。第二个多面体就是环面多面体。最近,我在研究一些和环面多面体相关的话题,在这里和大家分享一些我的发现。

我正在餐桌前吃早餐。餐桌上有一张圆形的大饼,有一个方形的蛋糕,还有一个甜甜圈。我依次思考了下面三个问题。你能帮我想出它们的答案吗?
提示:上一个问题的答案总会为下一个问题提供线索。
下图中的图 (a) 是由三个绳圈组成的。这是一个非常经典的图形,叫做 Borromean rings 。 Borromean rings 有一个非常神奇的特点:它们是套在一起的,没有哪个绳圈能从中取出来;但是,仔细观察你会发现,每两个绳圈之间都并没有直接套在一起!
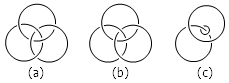
Borromean rings 还有一个听上去更离奇的性质:如图 (b) 所示,如果把其中任意两个绳圈真的套在一起,那么第三个绳圈就会自动脱落掉!为了看出这一点来,我们可以像图 (c) 那样,把其中一个绳圈缩小,让它紧紧地裹在另一个绳圈上,这下就很容易看出,它已经不再对第三个绳圈有任何限制作用了。
如果你喜欢上次的空间想象能力挑战,你一定会喜欢 V. V. Prasolov 的 Intuitive Topology 一书。书中的第一章有五个非常经典的“拓扑变换”类谜题,在此与大家分享。注意游戏规则:我们假设所有物体都是用橡胶做成的,可以随意地拉伸、挤压、弯曲,但不允许切断、粘连等任何改变图形本质结构的操作。
1. 能否把左图连续地变形为右图?

2. 能否把左图连续地变形为右图?

为了说明“同痕”这一概念直观上并不容易把握,《The Knot Book》一书中举了一个经典的例子。如下图,左图是一个有三个洞的立体图形,右图是被挖出了三条通道的立方体(但其中一个通道在另一个通道上缠绕了一圈)。令人难以置信的是,两者之间竟然是同痕的,换句话说前者可以连续地变形成为后者。你能想象出这个变换过程吗?
