你可以在这个Blog里看到很多地方用Mathematica代替了复杂的计算。Mathematica是一个强大的数学软件,很多网友看到了这个Blog上的一些演示后都迫不及待地装上了它。Mathematica的功能比你想象的多得多,今天我们来看一个有趣的Mathematica函数——Play函数。我们将用Mathematica做一些有关函数和声音的简单试验。
声音的实质是波函数。定义一个波函数和定义域的范围,Mathematica可以播放出它表示的声音。试在Mathematica中运行这条语句:
Play[Sin[4000 t], {t, 0, 2}]
=================== 我是可爱的分割线 ===================
上面的例子中,4000表示函数的周期大小,也就是声音的音调高低。把4000改成8000,你可以听到音调更高的声音:
Play[Sin[8000 t], {t, 0, 2}]
函数的形状决定了音色。对于不同的周期函数,声音是不一样的。试试下面三个不同的函数:
Play[Sin[5000 t], {t, 0, 2}]
Play[Tan[5000 t], {t, 0, 2}]
Play[Mod[5000 t, 50], {t, 0, 2}]
如果我们的函数不是周期函数呢?记得一次音乐课上,老师曾经告诉过我们音乐和噪声的区别。
Play[Random[], {t, 0, 2}]
=================== 我是可爱的分割线 ===================
音量的大小由振幅来控制,说穿了就是函数值的大小。运行下面三条语句,你会发现函数竟然可以用声音如此形象地表现出来。你甚至可以让别人根据音量变化来猜你放的是什么函数。
Play[Sin[4000t] t, {t, 0, 2}]
Play[Sin[4000t] t^2, {t, 0, 2}]
Play[Sin[4000t] Log[t], {t, 0, 2}]
Play[Sin[4000t] Sin[8t], {t, 0, 2}]
Play[Sin[4000t] Mod[t,0.4], {t, 0, 2}]
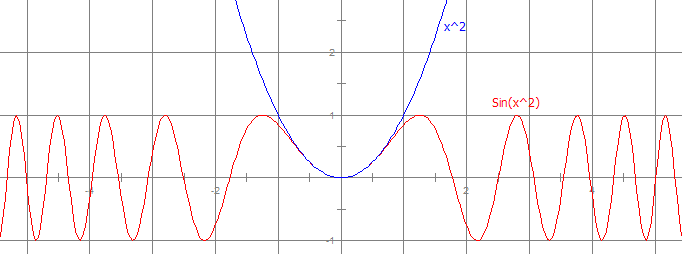
当复合函数出现后,真正有趣的事情开始了。我们来想象一下Sin(x^2)的图象是什么样子。x的绝对值越大,x^2的值变化越快,反映在正弦波上就是波长越短,音调越高。也就是说,x^2的形状与音高有直接的关系。于是,你将听到的是一段可以让你立即联想起二次函数的声音:
Play[Sin[5000 t^2], {t, -1, 1}]
在运行下面的语句前,你可以先自己想象一下每个函数对应的声音是什么样子的:
Play[Sin[5000/t], {t, 0, 2}]
Play[Sin[5000 * Sqrt[t]], {t, 0, 2}]
Play[Sin[5000 * Sin[4t]], {t, 0, 2}]
Play[Sin[2000 t * Sin[8t]], {t, 0, 2}]
=================== 我是可爱的分割线 ===================
两个函数相加的结果是什么?下面两个例子分别是二次函数加正弦函数,与倒数函数加噪声。你可以立即观察到,函数的相加即声音的相加。
Play[Sin[5000 (t-1)^2] + Sin[5000 * Sin[4t]], {t, 0, 2}]
Play[Sin[5000/t] + Random[], {t, 0, 2}]
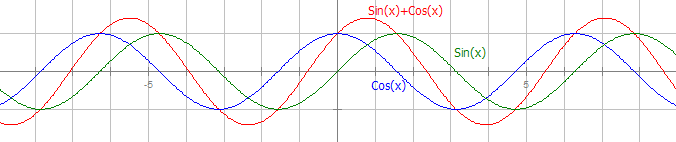
我们还可以举一些其它的例子来说明这种现象。比如,Sin[5000t]和Cos[5000t]的声音肯定是一样的,那么函数Sin[5000t] + Cos[5000t]的周期一定与原来相同,只是振幅更大。
再看下面的这个例子。同样是函数的相加,为什么这次只能听见mod函数的声音,但听不见正弦函数的声音呢?
Play[Sin[5000 t] + Mod[5000 t, 50], {t, 0, 2}]
原因很简单。上面两个函数中,mod函数的振幅更大,因此它的声音远远大于sin函数的声音,于是sin函数只能淹没在mod的嘈杂声中。如果把sin函数乘上一个系数50,两个函数的声音就一样大了:
Play[50 * Sin[5000 t] + Mod[5000 t, 50], {t, 0, 2}]
把倒数函数与噪声的五分之一相加,得到的就是一个带有轻微噪声的“倒数函数声”。
Play[Sin[5000/t] + Random[]/5, {t, 0, 2}]
=================== 我是可爱的分割线 ===================
当然,声音可以相加,也就可以相减。对于多种函数的混音,减去一个特定的函数可以从混音中踢去对应的声音。电影里经常会出现这样一些镜头,侦探们用电脑消去截获的音频中特定的背景声音。从函数的角度来看,这样的事情在理论上是可行的。比如,你偷偷摸摸录下了你的MM和她的前男友的谈话,但最关键的那段谈话声被一个突如其来的电话铃声盖住了。现在,你只需要获取一个电话铃声的样本,然后从原始声音中减去电话铃声即可。而电话铃声是非常简单的波函数,你完全可以自己生成一个。科幻电影中也经常见到一些类似的事情:某超级BOSS制造出的秘密武器可以放射有害波函数f(x),然后天才科学家们争分夺秒地制作并发射出-f(x)函数,企图和有害波正负抵消,把它中和了。在五花八门的波函数中加入一个-f(x),实际上就相当于从“混合波”中减去f(x)。
前几天给系里的MM找迎新晚会用的音乐伴奏时突然想到了一个有趣的问题:是否有可能在某个歌曲的原声和自己的清唱之间做差值运算?这在理论上提供了一个有趣的消音算法,和一个同样有趣的翻唱相似度评判标准(看差值里残留有多少人声)。
=================== 我是可爱的分割线 ===================
不要以为函数声音都那么难听,掌握适当的理论知识和技巧可以做出动听的声音。Mathematica的官方网站上有一个简单而动听的声音函数,这里写出来供大家欣赏:
Play[(2 + Cos[50 t])*Sin[2000*(1 + Round[2 t])*t], {t, 0, 3}]
Matrix67原创
转贴请注明出处
第一次涉及这方面的东西,很多东西都是自己的猜测,可能有理论错误,请大家指正!
同时,期待大家通过Mathematica试验发现更多有趣的推论。