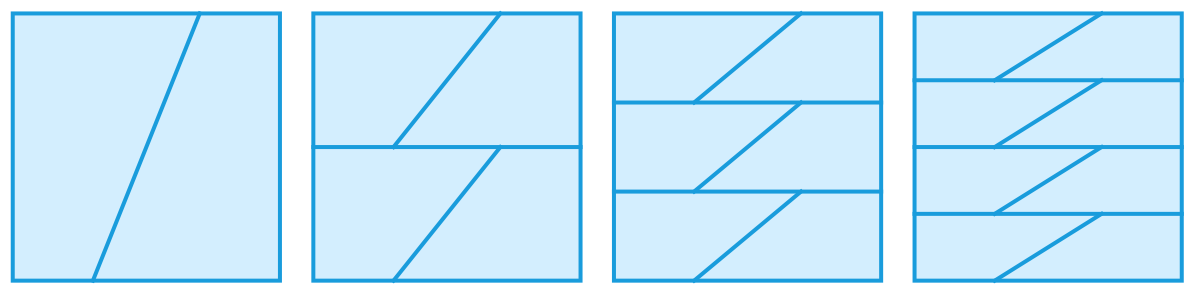
我们很容易在平面内放置很多点,使得任意两点确定的直线都只经过这两个点——你需要做的,仅仅是让任意三点都不共线就行了。那么,能否在平面内放置若干个点,使得任意两点确定的直线总是恰好经过三个点呢?更一般地,对于任意正整数 n > 2 ,能否在平面内放置若干个点,使得任意两点确定的直线总是恰好经过 n 个点呢?当然,我们要排除掉所有点都共线这种平凡的情况。
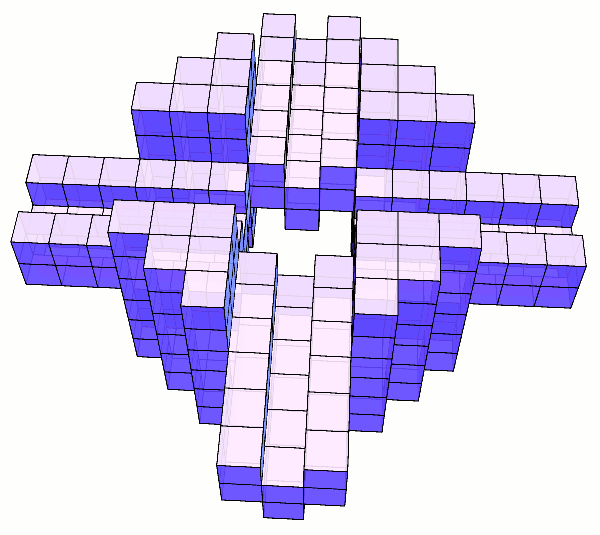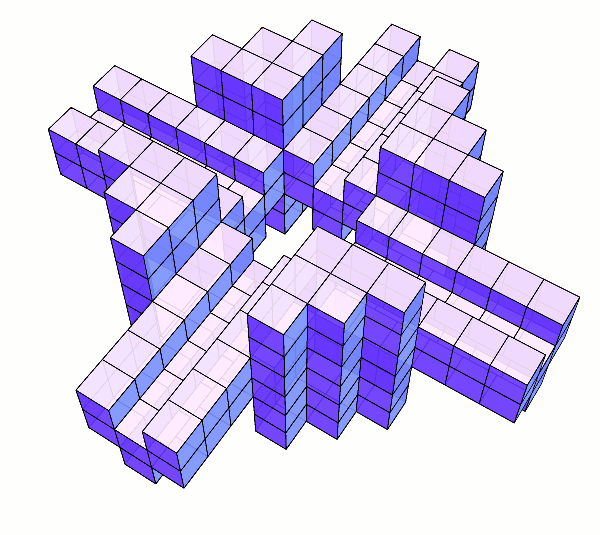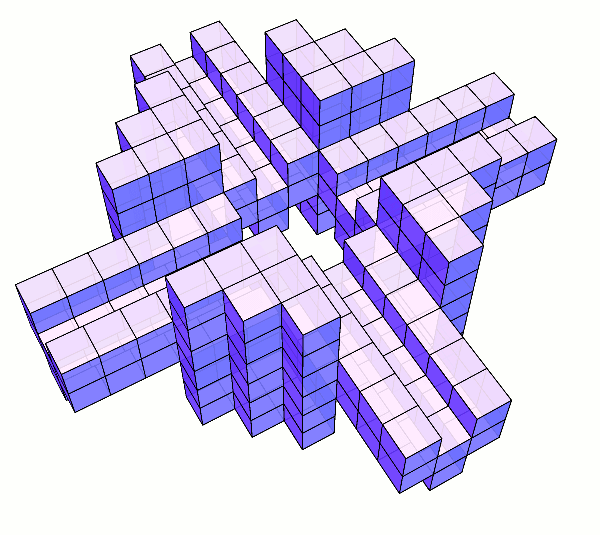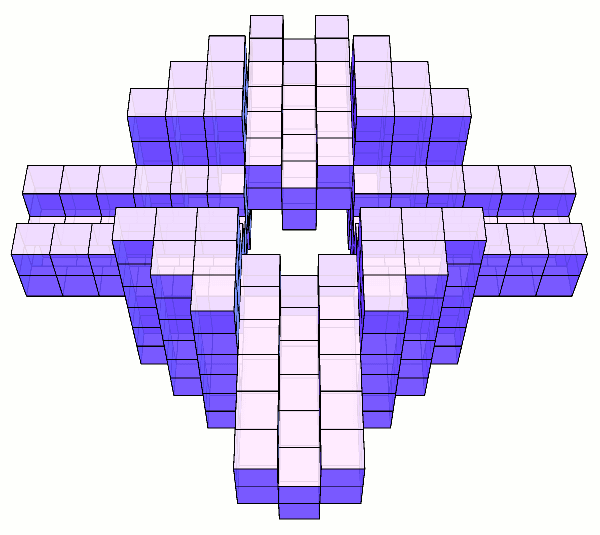
记得我很小的时候就想过这个问题。小时候有一种经典的智力题,大致就是叫你把多少多少棵树种成多少多少行,使得每行都有多少多少棵树。比方说,如何把 9 棵树种成 10 行,使得每行都有 3 棵树?答案如下图所示。但请注意,其实图中还有不少直线上只有 2 棵树,比如那条蓝色的虚线。
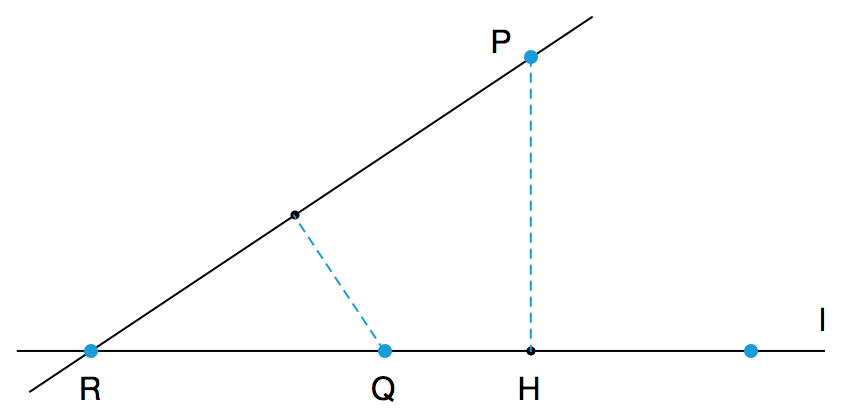
当时,我就曾经想过,如果树苗足够多,能否让每条可能的直线上都种有 3 棵树呢?于是,我没事儿就来尝试一番,但每一次都以失败告终。后来我才知道,这是不可能的。根据 Sylvester–Gallai 定理,在任意一个有限点集中,一定有一条直线恰好只经过两个点,除非所有的点都是共线的。这个定理有一个非常漂亮的证明,这里不得不提。假设存在某个点集,满足任意两点确定的直线上都存在其他的点。画出所有可能的直线,作出每一个点到每一条直线的垂线段,然后找出所有这些垂线段中最短的一条。不妨假设这条最短的垂线段是点 P 到某条直线 l 的垂线段,垂足点记作 H 。由假设, l 上至少有三个点,因此至少有两个点分布在垂足 H 的同一侧(允许和垂足重合)。不妨把这两个点记作 R 、 Q ,如下图所示。由于我们画出了所有可能的直线,因此 P 、 R 两点之间也有一条直线;此时, Q 到 PR 的垂线段就是更短的垂线段,于是产生矛盾。要想避免这样的矛盾,唯一的方法就是,所有的垂线段长度都为 0 ,换句话说我们根本作不出所谓的垂线段。这也就是所有点全都共线的情况。
我们刚才证明了,在一个点集中,只经过两点的直线一定存在,除非所有点全都共线;因此,当 n > 2 时,我们自然就无法让每条可能的直线上都有 n 个点,除非所有点全都共线。
Read more…