这是一个非常有趣的问题。许多快递公司都依据物件的长、宽、高三边之和来收费,一些航空公司也要求托运行李的三边长相加不能超过某个限制。那么是否有人想过,有没有可能把一个三边之和较大的盒子装进一个三边之和较小的盒子里,从而骗取更低的费用呢?有人会说,恐怕不行吧,长宽高之和更大的盒子体积不也应该更大一些吗?不见得。比方说,盒子A的长宽高分别是10、10、10,盒子B的长宽高分别是9、9、12.1。盒子B的三边长之和显然比盒子A要大,但体积只有980.1,比前者要小近20个单位。那么,为什么就不能把盒子B沿斜线方向塞进盒子A呢?有人会敏锐地发现,在上面的例子中,盒子A的体对角线长为17.3205,但盒子B的对角线长度达到17.5616,显然无法完全放进盒子A里。不过且慢,我也能举出这样的例子,三边和更大的盒子其体积和对角线都比小的盒子的要小。盒子A的长宽高分别为10、10、20,盒子B的长宽高分别为7.1、16.5、16.5。盒子B的长宽高之和比盒子A大,体积为1932.98,对角线长度比前者小大约0.1。看来,为了解决这个问题,我们还需要从一些更巧妙的方面入手。
惊奇数学事实
最近几天碰到的几个有趣的问题
最近几天见到了几道零散的、不成系统的趣题,在这里合成一篇文章,与大家分享。
1. 证明:对任意正整数n,n^2+n+1一定不是完全平方数。
2. 说一个实数是可表达的,当且仅当它能用有限长的语句明确地描述出来,如2147483648可以说成是“二的三十一次方”,√2即为“平方后等于二的正实数”,π即为“圆的周长和直径之比”。问题是,是否存在一个不可表达的实数?
3. 一个人有两个小孩儿,其中有一个生于星期二的男孩儿。问另一个是男孩儿的概率是多少?
4. 无需积分,计算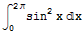 。
。
图表的重要性:Anscombe的四组数据
1973年,统计学家F.J. Anscombe构造出了四组奇特的数据。它告诉人们,在分析数据之前,描绘数据所对应的图像有多么的重要。
| I | II | III | IV | ||||
|---|---|---|---|---|---|---|---|
| x | y | x | y | x | y | x | y |
| 10.0 | 8.04 | 10.0 | 9.14 | 10.0 | 7.46 | 8.0 | 6.58 |
| 8.0 | 6.95 | 8.0 | 8.14 | 8.0 | 6.77 | 8.0 | 5.76 |
| 13.0 | 7.58 | 13.0 | 8.74 | 13.0 | 12.74 | 8.0 | 7.71 |
| 9.0 | 8.81 | 9.0 | 8.77 | 9.0 | 7.11 | 8.0 | 8.84 |
| 11.0 | 8.33 | 11.0 | 9.26 | 11.0 | 7.81 | 8.0 | 8.47 |
| 14.0 | 9.96 | 14.0 | 8.10 | 14.0 | 8.84 | 8.0 | 7.04 |
| 6.0 | 7.24 | 6.0 | 6.13 | 6.0 | 6.08 | 8.0 | 5.25 |
| 4.0 | 4.26 | 4.0 | 3.10 | 4.0 | 5.39 | 19.0 | 12.50 |
| 12.0 | 10.84 | 12.0 | 9.13 | 12.0 | 8.15 | 8.0 | 5.56 |
| 7.0 | 4.82 | 7.0 | 7.26 | 7.0 | 6.42 | 8.0 | 7.91 |
| 5.0 | 5.68 | 5.0 | 4.74 | 5.0 | 5.73 | 8.0 | 6.89 |
Pick定理的几个出人意料的应用
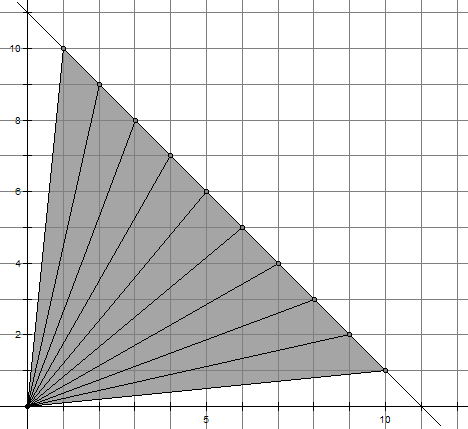
考虑直线x+y=n,其中n是一个素数。这条直线将恰好通过第一象限里的n-1个格点(如上图,图中所示的是n=11的情况)。将这n-1个点分别和原点相连,于是得到了n-2个灰色的三角形。仔细数数每个三角形内部的格点数,你会发现一个惊人的事实:每个三角形内部所含的格点数都是一样多。这是为什么呢?
