有一个放听装可乐的货架，它的宽度要比四听可乐的直径稍微大一些。把10听可乐放进这个货架里，堆叠成一个三角形。虽然底下三层可乐罐歪歪斜斜有高有低，但最顶上的那听可乐一定位于货架的正中心，也就是说它到货架两壁的距离是相等的。这是为什么呢？
惊奇数学事实
趣题：连续函数上的水平线段
连续函数f(x)满足f(0)=0且f(1)=0。证明，总能在[0,1]中找到两个数a和b满足b-a=1/2且f(a)=f(b)。换句话说，我们总能画出一条长为1/2的水平线段，它的两个端点都在函数f(x)上。
这个证明再次用到了我们上次提及的零点定理。考虑f(1/2)的值，如果它也等于0，我们的问题就直接解决了。无妨设f(1/2)>0，那么考虑f(x+1/2)-f(x)的值：当x=0时，该值为一个正数；但当x=1/2时，这个值变成了一个负数。这表明，在x从0增长到1/2的过程中，一定有某一刻使得f(x+1/2)-f(x)恰好为0。
我们接下来的问题是，除了长为1/2的横线段始终存在以外，还有哪些长度值具有相同的性质？下面我们证明，对任意一个正整数n，长为1/n的横线段也总是存在的。
零点定理的奇妙应用：平分面积的直线
零点定理是一个大家平时生活中用惯了以至于反而觉得很陌生的一个定理。若函数f(x)在区间[a,b]连续，并且f(a)与f(b)异号，那在(a,b)之间一定存在某个x，使得f(x)=0。如果你从海拔为-100的地方走到海拔为400的地方，那不管你是怎么走的，你一定会有经过了海平面的一瞬间。另一个比较隐蔽一些的应用便是，对任意一个凸多边形，总存在一条直线把它分成面积相等的两份。考虑一条竖直直线从左至右扫过整个凸多边形，则凸多边形位于直线左边的那部分面积由0逐渐增大为整个凸多边形的面积，直线右侧的面积则由最初的整个凸多边形面积渐渐变为0。若把直线左侧的面积记为f(x)，直线右侧的面积记为g(x)，则随着直线位置x的变化，f(x)-g(x)的值由一个负数连续地变为了一个正数，它一定经过了一个零点。这表明，在某一时刻一定有f(x)=g(x)。
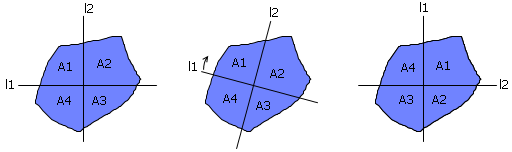
用类似的方法，我们能证明一个更强的命题：对任意一个凸多边形，总能用两条互相垂直的直线把它的面积分成四等份。利用前面的结论，我们能找到一条直线l1，它把整个凸多边形分成上下相等的两份；类似地，我们能找到唯一的一条与l1垂直的直线l2，使得它恰好把整个凸多边形分成左右相等的两份。注意，现在我们有A1+A2 = A2+A3 = A3+A4 = A4+A1，我们甚至立即还可以知道A1=A3并且A2=A4，但这都还不足以保证四块面积全都相等。怎么办呢？注意，我们前面假定直线l1是一条水平直线。事实上，l1每取一个方向，我们都能用上面的方法得到一个具有相同性质的新构造。为此，我们将直线l1的方向顺时针旋转90度。考虑整个过程中A1-A2的值的变化过程：旋转后的A1-A2恰好就是旋转前的A2-A3，而A1和A3又是相等的……于是我们发现，旋转前后的A1-A2的值恰好互为相反数！这表明，在直线l1旋转的过程中，一定有一瞬间满足A1-A2=0，这一刻的l1和l2便是两条互相垂直并把图形四等分的直线。
趣题：以无理点为圆心的圆周上最多有多少个有理点？
由于勾股数组有无穷多个，因此以原点为圆心的单位圆上有无穷多个有理点。例如，(3,4,5)是一组勾股数，因此(3/5, 4/5)就是单位圆上的一个有理点。将这个圆的半径放大有理数倍，则原来圆周上的有理点现在显然仍是有理点；将这个圆的圆心平移至一个有理点，则同样地，原来圆周上的有理点现在显然仍是有理点。于是我们得到这样一个结论：在平面直角坐标系内，任意一个以有理点为圆心，有理数为半径的圆周上总存在无穷多个有理点。我们不由得想到这样一个有趣的问题：如果一个圆的圆心是无理点（两个坐标中至少有一个不是有理数），那么圆周上的有理点个数还可能是无穷多个吗？若不是的话，最多能有多少个？
