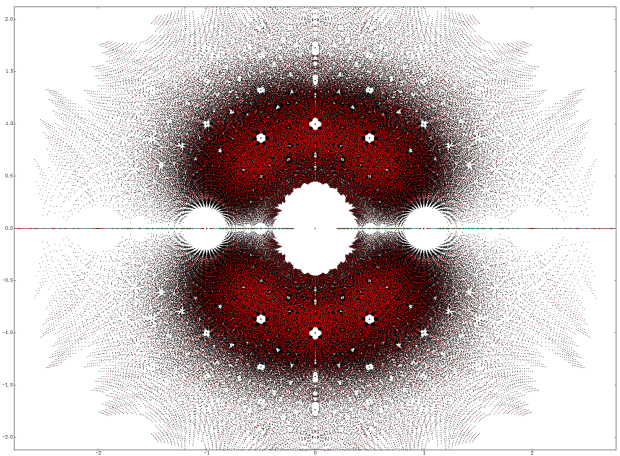
Dan Christensen发现，把所有次数不超过5的、系数在-4到4范围内的整系数多项式的所有根描绘在同一个复平面上，你会看到一个异常壮观的画面。图中的每个灰色点代表某个二次多项式的一个根，蓝色点代表三次多项式的根，红色代表四次多项式的根，黑色代表五次多项式的根。水平线代表实轴，0和±1的地方有很明显的空洞；竖直方向是虚轴，每个单位根处也都有明显可辨的空洞。
惊奇数学事实
Runge现象：多项式插值不见得次数越高越准确
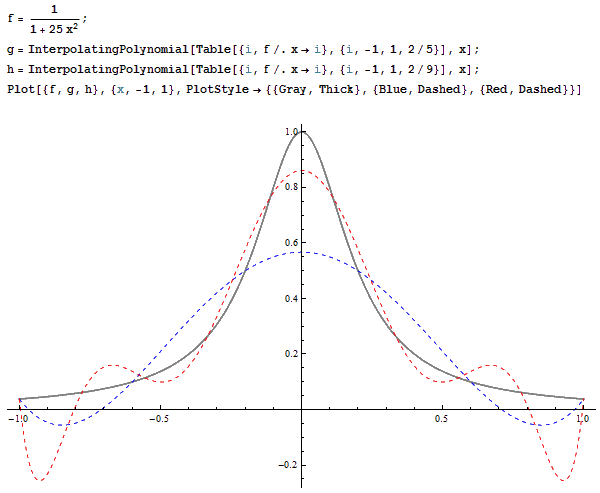
今天学到了一个新的名词，Runge现象。1901年，Carl David Tolmé Runge意外地发现，用差值插值多项式逼近函数f(x)=1/(1+25x^2)时出现了一些反常的现象。如图，灰色的粗线就是Runge函数在[-1,1]上的图象。蓝色虚线是过[-1,1]上的6个等距点所得到的5次多项式，红色虚线是过[-1,1]上的10个等距点所得到的9次多项式。可以看到，当次数变高时，插值多项式反而变得更不准确。
经典证明：任何可数集都含有不可数个嵌套子集
你相信吗？对于任意一个可数集，总能找出不可数个子集，使得从中任取两个集合，其中一个都是另一个的真子集。乍看之下，这似乎是不可能的。如果任两个集合之间都具有“其中一个是另一个的真子集”的关系，那它们就能构成一个“集合序列”（准确地说是全序关系），使得每个集合都是由它前面那个集合添加进若干元素得到；换句话说，我们能通过不断往一个空集中添加新的元素依次得到所有这些集合。但是如果这些集合中的元素就只有可数个，那这个“集合序列”中怎么会有不可数个集合呢？然而，涉及到无穷的问题总是那样违背直觉。下面我们只用三行字就能说明，这个命题的的确确是成立的。
Buffon投针实验：究竟为什么是pi？
重要通告：最近多次发现我的tom邮箱发出的邮件被识别成了垃圾邮件，是什么原因我还不是很清楚。最近向我的tom邮箱发过邮件但迟迟没有收到回复的朋友麻烦检查一下垃圾邮件箱，或者重新给我发一次邮件，我换一个邮箱回复您。
数学学习真正悲哀的就是，记住了某个神奇而伟大的定理，看懂了其最严密的推导过程，但却始终没能直观地去理解它。虽然严密的推导是必要的，直观理解往往是不准确的，但如果能悟出一个让定理一瞬间变得很显然的解释，这不但是一件很酷的事，而且对定理更透彻的理解和更熟练的运用也很有帮助。我惊奇地发现，国内的每一本高数课本上都严格地讲解了微积分基本定理的证明，但几乎没有任何一个课本上讲过积分等于函数下方的图形面积究竟是为什么。事实上，这几乎是显然的，但还是有不少人学完微积分后仍然没有意识到。每当谈到这个问题时，我更愿意首先提出一个非常有启发性的事实——圆的周长是2·pi·r，圆的面积就是pi·r^2，后者的导数正好就是前者。这个现象是很容易理解的，因为圆的半径每增加一点，面积增加的就是周长那么一圈，换句话说面积的变化就等于周长。类似地，如果你能找到一个函数g(x)，它的导数正好就是f(x)，那么当x每增加一点，g(x)就增加了一条小竖线段，显然g(x)就应当是f(x)下方的面积。看清了这一点之后，我们才能欣赏到微积分基本定理真正牛B的地方。原先大家都是用分割求极限的办法来求函数下方的面积，但Leibniz却把面积看作一个可变的整体，用一种办法“一下子”就把它求了出来。有趣的是，这种现在看来如此自然的神奇办法，一千多年来居然没有任何人想到。
把[0,2]分割为可数个部分 然后拼成全体实数集R
Banach-Tarski悖论指出，你可以把一个三维球体分割成有限多份，然后拼合成两个和原来一模一样的球体。这个构造是Stefan Banach和Alfred Tarski在1924年发表的论文中给出的，不过我还从来没有完整地瞻仰过这个牛B的构造过程。今天我看到了一个Banach-Tarski悖论的弱化版，但它的反直觉性绝对不亚于Banach-Tarski悖论。通过这个弱化的结论，你或许会对Banach和Tarski的构造方法有了更多的理解。
下面我将会给出这样一个神奇的构造：取出[0,2]的一个子集S，把它分割为可数个不相交的点集，对每个点集各自进行适当的平移后，可以让它们的并集变为全体实数集。