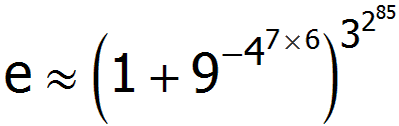
刚才看到这个很漂亮的无理数 e 的近似表达,它恰好用到了 1 到 9 这 9 个数字。
猜猜看它能精确到 e 的小数点后多少位? 10 位? 100 位? 1000 位? 10000 位?
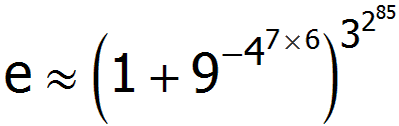
刚才看到这个很漂亮的无理数 e 的近似表达,它恰好用到了 1 到 9 这 9 个数字。
猜猜看它能精确到 e 的小数点后多少位? 10 位? 100 位? 1000 位? 10000 位?
承认选择公理可能给我们带来很多有悖于直觉的结论。最著名的例子可谓 Banach-Tarski 悖论了:你可以把一个三维的实心球分成有限多块,通过刚体移动把它变成两个和原来一模一样的球。本 Blog 还介绍过另外一个有趣的结论,它违背常理的程度也不亚于 Banach-Tarski 悖论。今天,我给大家看一个比这些悖论更加荒唐的结论:利用选择公理,我们可以实现预测未来!
在探讨这个话题之前,我们得先为“预测未来”建立一个合理的数学模型。我们假设,对于任一时刻,宇宙中的所有信息都可以编码为某个状态值,我们就把它叫做宇宙的一个“点状态”。宇宙中所有可能的点状态就组成了宇宙的“状态集合”。以数学的眼光看宇宙,一个宇宙也就无非是一个一元函数 f(t) 。它的定义域是整个时间轴 R ,它的值域是宇宙的状态集合,预测未来也就仅仅是根据已知的函数值来推测未知的函数值罢了。假设我们已经知道在区间 (-∞, t0) 上函数的所有取值,如果你能据此给出 f(t0) 的精确值,我们就说你成功地预测了 t0 时刻的宇宙状态。当然,仅凭借过去的信息你是不可能保证猜对 t0 时刻的点状态的,例如对于两个只在 t0 处有区别的宇宙,算法最多只能猜对其中一个宇宙在 t0 处的状态。但你相信吗,存在一个算法,使得我能正确预测几乎所有时间点的宇宙状态。换句话说,我能构造出这样一个算法,使得除了可数个点以外,给定任意一点以前的全部函数值,我都能套用该算法猜对该点的点状态。再换句话说,利用这个算法预测任意时刻的宇宙状态,成功的概率为 1 。
下面是一个有趣的小把戏:拿出一个科学型计算器(就比如说 Windows 计算器),确认你的计算器使用的是角度制。然后,输入 55555555 ,按 1/x ,再按 sin ,然后看看你的屏幕……神奇吧!如果你觉得还不够精确,输入 55555555555555555555 ,再依次按下 1/x 和 sin 看看……
事实上,sin( (1 / 55555555555555555555)° ) = 3.141592653589793238494059.. * 10-22 ,前 20 位都和 pi 的值一模一样。显然,这绝对不可能是一个巧合。那么,这究竟是为什么呢?
注意到 1/180 = 0.00555555… ,换句话说 55555..55 (连续 n 个 5 )的倒数就近似于 180 * 10-n-2 。另外,当 x 很小很小的时候, sin(x) 会与 x 非常接近,但在角度制中,我们必须写作 sin(x) ≈ (pi / 180) x 。因此, sin(1 / 55555..555) ≈ (pi / 180) * (180 * 10-n-2) = pi * 10-n-2
来源:http://divisbyzero.com/2010/02/17/the-math-behind-a-neat-calculator-trick/
Math Horizons 杂志 2010 年 4 月刊上发表了一个有点搞笑的题目,很有些愚人节玩笑的味道。
观察下面这个分式方程:
它可以化简为 x^3 – 42x + 36 = 0 ,如果分式方程存在整数解,这个解一定是 36 的约数。把 36 的约数一个一个代进去便可得到,这个分式方程的唯一整数解为:
现在,你能快速求解出下面这个方程的整数解吗?
只需要注意到,新的分式方程是由原方程旋转 180 度得到的,因此它的解应该为:
有意思的是,这个“推导”虽然是荒谬的,但 x = 9 真的就是第二个方程的唯一整数解!
来源:http://www.cut-the-knot.org/proofs/FalseSymmetry.shtml
大家或许知道 Banach-Tarski 悖论——把一个三维球分成有限多份并重新拼成两个和原来一模一样大的球——这个悖论告诉我们利用选择公理我们能够推出看上去多么不合逻辑的东西。今天我听说了另一个类似的悖论叫做 Sierpinski-Mazurkiewicz 悖论,它的结论在直观上同样令人难以接受,并且推导不依赖于选择公理。
Sierpinski-Mazurkiewicz 悖论是说,存在平面上的一个点集 S ,我们能把它划分成两个子集 A 和 B ,使得 A 旋转 1 弧度后与 S 完全重合, B 平移一个单位后也与 S 完全相同。换句话说,存在这么一个点集,我们能把它分成两个与自身一模一样的子集!这听上去实在是不可思议,然而构造却极其简单。