考考你的立体几何直觉:用一系列间距相等的平行平面把一个球体切成厚度相同的薄片,这些薄片的侧面积都相等吗?
惊奇数学事实
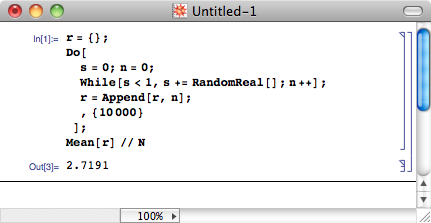
惊人的答案:平均要取多少个(0,1)中的随机数才能让和超过1
数学常数最令人着迷的就是,它们常常出现在一些看似与之毫不相干的场合中。 随便取一个 0 到 1 之间的数,再加上另一个 0 到 1 之间的随机数,然后再加上一个 0 到 1 之间的随机数⋯⋯直到和超过 1 为止。一个有趣的问题:平均需要加多少次,才能让和超过 1 呢?答案是 e 次。
火柴棒搭成的几何世界
前几天,我看到了这样一个问题:如何用火柴棒准确地搭出一个正方形?注意,由于没有任何工具可以让两根火柴棒拼成一个 90° 角,因此用四根火柴棒随意摆出一个四边形,最多也只能是个菱形。要想拼出一个正方形,我们还得想些奇招来。
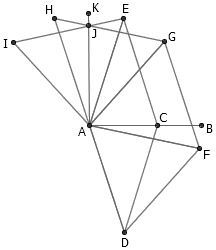
一个经典的做法如上图所示。先摆出线段 AB ,下面我们将要确定线段 AK 的位置,使得两条线段成 90° 角。在 AB 上随意找一个点 C ,以 AC 为底搭出两个腰为 1 的等腰三角形 DAC 和 EAC 。容易看出, D 、 E 是关于 AB 对称的两个点。搭建一系列等边三角形 △ADF 、 △AFG 、 △AGH ,确定出 D 关于 A 点的对称点 H 。这样, H 、 E 两点就关于 AK 轴对称了。再搭一个等边三角形 AIE ,则 I 、 G 两点也关于 AK 对称。因此, HG 和 IE 的交点 J 就在 AK 上,自然 AK 的位置也就确定出来了。重复执行以上操作,我们便能完成以 AB 为边的整个正方形。
连杆系统:比你想象中的更强大
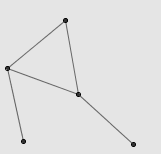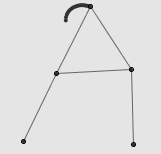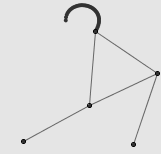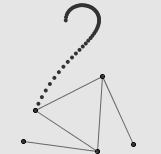
在机器时代,作为机械构造的理论工具,连杆系统曾一度成为数学界中最热门的话题。所谓连杆系统,就是一些刚性的小杆在端点处以转轴的方式相连,形成的一个机械装置。固定某些顶点的位置之后,其余的动点就能画出一些有趣的轨迹。比方说,固定线段 AB 的其中一个端点 A ,则顶点 B 将描绘出一个绕 A 点的圆周。


连杆系统最激动人心的,莫过于一些简单的连杆装置能够描绘出非常复杂的曲线。例如,上面的右图就是由五根相同长度的线段构成的连杆。固定 A 、 B 两个端点后,显然 C 和 D 描绘出的都是圆弧,但 E 点的轨迹就很难以想象了。事实上, E 点的轨迹相当的诡异,需要用一些复杂的代数语言才能描述。
用一张日落照片估算出地球的半径
你相信吗,仅仅利用一张日落的照片,你就能得出地球的半径大小! Princeton 大学的 Robert Vanderbei 在最近的一篇论文中对一张摄于密歇根湖的日落照片进行了分析,不但证实了地球是圆的,还依据照片上的内容对地球半径进行了估算。我把计算的大致过程向大家描述一下,供大家膜拜。

事情的起因就是上面这张很平常的日落照片,以及这样一个大家平时并没有太在意的问题:太阳露出水面的部分应该是一个标准的弓形,但为什么在日出日落时,我们所看到的太阳是一个橄榄球一样的形状?大家或许会很快想到,发光体的下半部分其实是日光反射在水面上造成的。随之产生的是另一个问题:为什么它的下半部分要比上半部分小一些呢?
