看到新词就上一下Wikipedia确实是一个好习惯。前一篇日志的那个pdf里作者提到了Gedankenexperiment(Thought experiment)，上Wikipedia一查果然学到了牛B的新东西。好多物理定律其实完全是由思维实验推导出来的，难以置信仅仅是思考竟然就能得出物理世界遵从的各种法则。经典的物理思维实验有Newton大炮、Galileo斜塔实验、Schrödinger的猫猫、Maxwell的妖怪等等。还有，Turing机也是一个伟大的思维实验。

   
    数学上的不少悖论（特别是涉及到维度和无穷的悖论）都是相当有趣的思维实验。Gabriel喇叭是y=1/x在[1,+∞)上的图象沿x轴旋转一周所形成的旋转体。这个简单的三维图形有一个奇特的性质：它的表面积无穷大，却只有有限的体积。为了证实这一点，只需注意到：
   
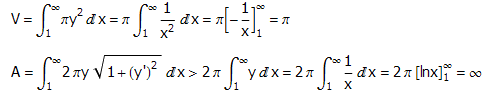
    Gabriel喇叭会导出一个非常诡异的悖论：如果你想用涂料把Gabriel喇叭的表面刷一遍，你需要无穷多的涂料；然而把涂料倒进Gabriel喇叭填满整个内部空间，所需要的涂料反而是有限的。
    有网友一定会问，那有没有什么二维图形，面积有限大，周长却无限长呢？答案是肯定的，Koch雪花就是这样一个经典的例子。不过，通过分形构造出来的这类图形似乎并不存在涂料悖论，因为递归到一定深度时分形图形的尺度将小于表面涂料的厚度，因此表面大小不能永无止境地算下去，涂满表面所需的涂料不再是无穷多。当考虑到涂料厚度时，原先的悖论也可以解释清楚了：填充内部空间仅仅涂满了图形的内表面，一旦考虑到涂料的厚度，它和外表面的区别就出来了。

Read more…

    我们想要计算无穷级数Σ(1/n)*(-1)^(n+1) = 1 – 1/2 + 1/3 – 1/4 + 1/5 – 1/6 …。首先我们需要说明，这个无穷级数是收敛的。注意到，从1的后面开始，每减去一个数后紧接着都会加上一个比它小的数，因此不管你加到哪儿，它的和始终不会超过1；另外，从1-1/2之后开始，每加一个数紧接着都会减去一个比它小的数，因此无论加到什么位置，整个和始终大于1/2。这说明，这个级数是收敛的，并且它收敛到1/2和1之间的某个数（事实上这个数是ln(2) ）。

    好了，令这个无穷级数为S，现在对S进行这样的变换：

S = 1 – 1/2 + 1/3 – 1/4 + 1/5 – 1/6 + …
  = (1 + 1/3 + 1/5 + 1/7 + …) – (1/2 + 1/4 + 1/6 + 1/8 + …)
  = (1 + 1/3 + 1/5 + 1/7 + …) – (1/2 + 1/4 + 1/6 + 1/8 + …) + (1/2 + 1/4 + 1/6 + 1/8 + …) – (1/2 + 1/4 + 1/6 + 1/8 + …)
  = (1 + 1/2 + 1/3 + 1/4 + …) – 2 * (1/2 + 1/4 + 1/6 + 1/8 + …)
  = (1 + 1/2 + 1/3 + 1/4 + …) – (1 + 1/2 + 1/3 + 1/4 + …)
  = 0

    但刚才不是说了S是大于1/2的么？这怎么可能呢？

Read more…

    去年的一篇日志里给大家推荐了几段非常神奇的音频，这里也有一个很不可思议的声音错觉。今天看到了另一些有趣的声音错觉，和大家分享一下。
    准备好一副高质量的耳机哦。

语音幻象：http://philomel.com/phantom_words/example_phantom_words.php
    你的大脑会自动地尝试把一些无意义的声音转换为有意义的语音。在这段音频中你可能会觉得你听到了一些单词，事实上这些单词都是不存在的，这段声音没有任何意义。
    不同的人所感觉到的单词是不同的。大多数人认为自己听到了下面这些单词中的某一个：
    window, welcome, love me, run away, no brain, rainbow, raincoat, bueno, nombre, when oh when, mango, window pane, Broadway, Reno, melting, Rogaine

低音在哪一边：http://philomel.com/musical_illusions/example_scale_illusion.php
    戴上耳机听。猜猜看低音是在左声道还是右声道？取下其中一边的耳机，只听另一个声道，你会发现实际上的声音和你预想的完全不一样。这段音频也有类似的效果。

语流的短时诱导：http://www4.uwm.edu/APL/audioBook/11Phon_Rest_Single.mp3
    我们的大脑会自动填上语音间的空隙。Richard Warren发现，把一段连贯的语音中的个别音节（准确地说是音位）替换成咳嗽声，被试者仍然能够准确地复述刚才听到的句子，而且说不出究竟是哪个音节被替换了。但如果用一段空白音来代替咳嗽声，则多数人都能够分辨出消失的是哪一个音节。

三全音悖论：http://philomel.com/musical_illusions/play.php?fname=Tritone_paradox
    对于同一组音调，一些人认为后一个音比前一个音高，另一些人则认为后一个音比前一个音更低。这里有一些详细的解释。为什么我怎么听都觉得后一个音总是比前一个音高？

混乱的旋律：http://philomel.com/musical_illusions/play.php?fname=Mysterious_melody_scrambled
    这段声音向我们展示了，八度音的变化将对我们的听觉造成怎样的影响。这是一段你保证听过的旋律，所有的音都是对的，只是它们随机地分布在了三个八度音里。你能听出这是什么音乐吗？

    无穷个囚犯面向数轴的正方向依次就座，第i个囚犯坐在数轴上坐标为i的地方，他可以看见所有坐标大于i的囚犯头顶上的帽子。看守给每个囚犯戴上黑色或白色的帽子，然后依次叫每个囚犯猜测自己头上的帽子颜色，猜对了的予以释放。另外一点和原来不同的是，囚犯们不能听到其他人的猜测。另外注意到，由于每个人前面都有无穷多个人，因此囚犯们无法通过数他前面的人数来判断出自己的位置，于是我们不得不加上一句：每个人都知道他后面有多少人（即他是第几个被问的）。同样地，事先所有囚犯可以商量出一个策略。你认为这下囚犯们还有什么好办法没？
    这下囚犯已经不能通过自己的猜测来通风报信了，似乎每个人都只能瞎猜，任何人都无法保证自己能猜对。你相信吗，居然有这样的策略，它可以保证除了有限个囚犯之外，其他囚犯全部释放！
    考虑所有可能的颜色序列（你可以简单地想像成01串）。我们说两个颜色序列“无穷远相等”，如果经过了有限多项之后，余下的无穷多项完全相同（即存在某个数x，使得两个串在各自的第x位后面完全重合）。这种关系显然满足自反性、对称性和传递性，是一种等价关系。因此，按照这种有限位后对应相等的关系，我们可以把所有可能的颜色序列划分为一个个等价类。它们的交集为空（两个等价类如果有交集，由传递性它们立即并成了一个更大的等价类），并集为全集（若某序列不属于任何等价类，则它自己就是一个新的等价类），是全集的一个划分。你能想象出一个等价类大致是什么样子的吗？假如把同一个等价类里的所有序列对齐并排放在一起，你从前往后走过去的时候会发现这些序列“越来越相像”。你走得越远，你会发现越来越多的序列开始变得互相重合；当你走到无穷远时，所有的序列都变成一个样了。
    囚犯们事先在每一个等价类中选一个代表元，然后把所有等价类的代表元背下来。到时候，每个人都能够看到他前面无穷多个人的帽子颜色，并且知道他自己在整个序列的位置，于是能立即判断出他们现在所处的颜色序列在哪个等价类里。接下来，他们只需要按照事先背好的代表元来猜就行了。由“无穷远相等”的定义，经过有限次猜测后最终这个代表元会和他们所处的序列重合，于是除了前面有限多个人以外，以后无穷多个人都可以保证猜对。

    你是否觉得这种“策略”很不合理，虽然从逻辑上看每一步推理都是无懈可击的？有人认为，这是选择公理带来的悖论。选择公理是说，给你一系列的集合（可能有无穷多个），那么我们总可以在每一个集合里取出一个元素来。这并不是显然正确的。你不可以依次考虑每个集合，从里面随便取出一个元素来，因为集合个数有可能无穷多个（甚至不可数），这样的操作将永无止境，不允许出现在数学推理过程中。我们需要定义一套系统，使得它对于给定的每一个集合都适用，这样我们就可以“一下子”处理完所有的集合。换句话说，对于一组数量任意多的集合，我们需要定义一个函数f，使得对其中任一集合S，f(S)为S里的一个元素。我们称函数f为选择函数。例如，给出自然数集的所有子集，选择函数f可以定义为“集合中的最小元素”；给出实数集的所有有限长的区间，则选择函数f可以定义为“区间的中点”。但对于某些情况，目前还没有办法用之前已有的公理系统定义出合适的选择函数。比如，目前仍然不清楚，对于实数集的所有非空子集是否存在一个选择函数。但选择函数的存在是很多数学推理的前提假设。因此，我们有必要承认选择公理，构成新的公理体系（即ZFC公理体系）。于是在今后的数学推理中，我们可以假设存在这样一个超级选择函数f，它就是专门用来干这破事的。承认选择公理有可能推出一些与生活经验背道而驰的结论，最著名的就是Banach-Tarski悖论：你可以把一个三维球体分成有限多块，然后拼接组合成两个和原来一样大的球体。上面所提到的100囚犯问题加强版则是选择公理带来的另一个悖论。

参考资料：http://cornellmath.wordpress.com/2007/09/13/the-axiom-of-choice-is-wrong （墙就是强）