悖论
用选择公理来预测未来
承认选择公理可能给我们带来很多有悖于直觉的结论。最著名的例子可谓 Banach-Tarski 悖论了:你可以把一个三维的实心球分成有限多块,通过刚体移动把它变成两个和原来一模一样的球。本 Blog 还介绍过另外一个有趣的结论,它违背常理的程度也不亚于 Banach-Tarski 悖论。今天,我给大家看一个比这些悖论更加荒唐的结论:利用选择公理,我们可以实现预测未来!
在探讨这个话题之前,我们得先为“预测未来”建立一个合理的数学模型。我们假设,对于任一时刻,宇宙中的所有信息都可以编码为某个状态值,我们就把它叫做宇宙的一个“点状态”。宇宙中所有可能的点状态就组成了宇宙的“状态集合”。以数学的眼光看宇宙,一个宇宙也就无非是一个一元函数 f(t) 。它的定义域是整个时间轴 R ,它的值域是宇宙的状态集合,预测未来也就仅仅是根据已知的函数值来推测未知的函数值罢了。假设我们已经知道在区间 (-∞, t0) 上函数的所有取值,如果你能据此给出 f(t0) 的精确值,我们就说你成功地预测了 t0 时刻的宇宙状态。当然,仅凭借过去的信息你是不可能保证猜对 t0 时刻的点状态的,例如对于两个只在 t0 处有区别的宇宙,算法最多只能猜对其中一个宇宙在 t0 处的状态。但你相信吗,存在一个算法,使得我能正确预测几乎所有时间点的宇宙状态。换句话说,我能构造出这样一个算法,使得除了可数个点以外,给定任意一点以前的全部函数值,我都能套用该算法猜对该点的点状态。再换句话说,利用这个算法预测任意时刻的宇宙状态,成功的概率为 1 。
Sierpinski-Mazurkiewicz悖论:一加一还是等于一
大家或许知道 Banach-Tarski 悖论——把一个三维球分成有限多份并重新拼成两个和原来一模一样大的球——这个悖论告诉我们利用选择公理我们能够推出看上去多么不合逻辑的东西。今天我听说了另一个类似的悖论叫做 Sierpinski-Mazurkiewicz 悖论,它的结论在直观上同样令人难以接受,并且推导不依赖于选择公理。
Sierpinski-Mazurkiewicz 悖论是说,存在平面上的一个点集 S ,我们能把它划分成两个子集 A 和 B ,使得 A 旋转 1 弧度后与 S 完全重合, B 平移一个单位后也与 S 完全相同。换句话说,存在这么一个点集,我们能把它分成两个与自身一模一样的子集!这听上去实在是不可思议,然而构造却极其简单。
拥有多个A的概率:又一个条件概率悖论
概率论给我们带来了很多匪夷所思的反常结果,条件概率尤其如此。网络上每一次有人发帖提出与条件概率有关的悖论时,总会引来无数人的围观和争论,哪怕这些问题的实质都是相同的。
来看两道简单的组合数学问题:
1. 四个人打桥牌。其中一个人说,我手上有一个A。请问他手上有不止一个A的概率是多少?
2. 四个人打桥牌。其中一个人说,我手上有一个黑桃A。请问他手上有不止一个A的概率是多少?
这两个问题看起来很像,实际算法大不相同。在第一题问题中,
手上一个A也没有 有 C(48,13) 种情况
手上有至少一个A 有 C(52,13) – C(48,13) 种情况
手上恰好有一个A 有 C(48,12) * 4 种情况
手上有至少两个A 有 C(52,13) – C(48,13) – C(48,12) * 4 种情况
根据条件概率公式,手上有超过一个A的概率为(C(52,13) – C(48,13) – C(48,12) * 4) / (C(52,13) – C(48,13)) = 5359/14498 ≈ 37%
无限长的金属杆:理想模型带来的悖论
有些时候,数学模型和物理世界相结合可能会得出一些不可思议的悖论,Gabriel喇叭就是最经典的例子。这里,让我们来看另一个有趣的例子。
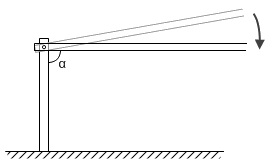
假设有一个无穷大的桌面,上面垂直地树立着一根有限长的金属杆。在这根金属杆的顶端用铰链连接一根无穷长的金属杆。这根无穷长的金属杆可以绕着活动关节处上下转动。让无穷长的金属杆随重力自由活动。注意到夹角α绝对不可能小于90度,因为我们的金属杆和桌面都是理想刚体,它们不能相交、穿透。这样的话,α只可能是90度。于是,荒唐的一幕发生了:这根无穷长的金属杆平行地悬在桌面上空,但却只有端点处这一个支撑点。
来源:http://www.cut-the-knot.org/WhatIs/Infinity/InfiniteRod.shtml