微积分
经典证明:质数无穷多与两个更强的命题
又回来更新啦!虽然还有两门课没考,但今天已经轻松了不少。梦魇般的现代文学史总算是结束了。抱了两天两夜的佛脚,结果考试时一看卷子,仍然没一道会的题目。不定项选择多选少选均不得分,都是些文学常识题,给四篇我从没见过的小说名字问哪些是第一人称叙事,或者给四个人名字问哪些是笔名之类的。天哪……以后的古代文学史咋办啊。
先强烈推荐一本好书。前几天在TopLanguage看到有牛人推荐Proofs from THE BOOK这本书,当即决定买了下来。这几天复习累了我都在看这本书,真的是很好很强大,里面汇集了很多著名问题的经典证明,包括很多我一直想找但没找到的证明。好了不多废话了,下面进入正题。
很早以前,我们曾经研究过质数,证明了质数有无穷多个。后来,我们又学到了另外两种证明质数无穷多的方法。这两种方法的基本思路相同:寻找一个无穷大的集合,里面的数两两互质。只用有限个质数明显不能得到无穷多个两两互质的数,于是我们立即可知质数必然有无穷多个。今天,我们将证明两个比质数无穷多更强的定理。这两个证明都出自Proofs from THE BOOK的第一章。
定义函数π(x)为“小于等于x的质数有多少个”。无妨规定x为一个正整数。我们将用初等微积分方法证明当x趋于无穷时π(x)也趋于无穷并给出π(x)的一个下界。我们将说明,对于所有x,π(x)>=log(x)-1,即x以内的质数至少有log(x)-1个。
为了说明这一点,让我们考虑所有不超过x的质数的倒数的等比级数(1 + 1/p + 1/p^2 + ..)的乘积,即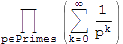 。
。
回忆等比级数的公式,则我们有:
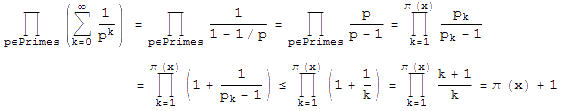
第二行的一些变换非常巧妙。第二行中间的不等号是一个关键,用到了一个基本事实:第k个质数显然比k大。最后的连乘中前一项的分子和后一项的分母正好抵消,最后消完了就只剩了一个π(x)+1。
另一方面,想像一下把(1+1/2+1/4+…)(1+1/3+1/9+…)(1+1/5+1/25+…)…展开的样子,很显然展开后的每一项都是一个所有质因子都不大于x的数的倒数,即Σ(1/m),其中m取所有仅含1..x范围内的质因子的数。显然,原本就比x小的数,其质因子当然不可能超过x,这就是说从1到x的所有正整数都是属于m的。利用一些微积分的基本知识,我们可以立即得出Σ(1/m) >= 1+1/2+1/3+…+1/x >= log(x)。地球人都知道,log(x)是没有上界的,于是质数的个数也没有上界。
这里还有一个类似的问题,大家可以对照着看看。
物理方法解决数学问题(二):Archimedes与球体积公式
我们平时习惯说“微积分”。有趣的是,积分的出现远远早于微分。积分思想的早期萌芽甚至可以追溯到古希腊时代,Democritus曾运用这种思想解决了很多复杂的问题。他的“数学原子论”观点强调几何体是由一个一个面重叠而成,而面则是由线组成。他把圆锥看作一个个不可再分的薄片,从而成功地得到了圆锥体体积公式:圆锥的体积等于等底等高的圆柱体体积的1/3。事实上,仅仅凭借经验加实验,这个公式也很容易被发现,因此我们这里不再仔细追究公式的推导过程。但古希腊人对球体积的研究却迟迟没有进展。此时,一代神牛Archimedes出现了。Archimedes用了一种出人意料的神奇方法找到了球的体积公式,整个推导过程令人称叹不已,拍案叫绝。
我们从圆的方程开始说起。首先观察方程(x-a)^2 + y^2 = a^2,这是一个中心在(a,0),半径为a的圆,它在y轴右边与y轴相切。整理一下这个式子,我们有x^2 + y^2 = 2ax。在这个式子中,x可以从0取到2a,每一个x的值就对应着一个y值,它表示圆上对应位置的半弦长。注意到这个式子的特殊性:如果等式两边同时乘以π,牛B东西就来了:πx^2 + πy^2 = 2aπx,左边出现了两个与圆面积相关的项。这使我们有了一种让等式两边再乘以一个2a的冲动,因为这样的话等式右边也出现了一个与2a相关的圆面积:2a(πx^2 + πy^2) = x π(2a)^2。现在的问题是,等式左边多出来的一个2a和等式右边的那个x该咋办?不用担心,我们不是有杠杆原理这种牛B东西么,这两个东西可以当力臂长啊。于是,一个现在看上去并不算太突兀的力学模型出现了:
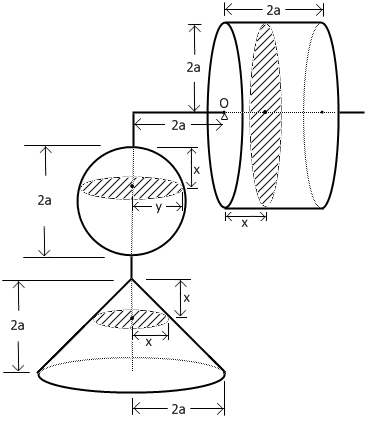
找一根不计重量的金属杆,水平放置这根金属杆并以O为支点。金属杆右边串一个半径和高都是2a的圆柱体,圆柱体的左端点与支点O重合。把一个半径为a的球和一个底面半径和高都是2a的圆锥用绳子串起来,悬挂在左边距支点2a处。再次回到我们刚才的等式2a(πx^2 + πy^2) = x π(2a)^2。发现了吗,每取一个x,式子中的三个圆面积公式正好对应着这三个几何体相应位置上的横截面积。右边的圆柱横截面积始终为π(2a)^2,它离原点的距离为x;左边那个圆锥的横截面积为πx^2,它与圆锥顶端的距离为x;圆锥上方的那个球里同样存在一个对应的截面,这个截面离球的顶端距离也是x,而它的面积则正好是πy^2(回忆之前提到的半弦长)。乘上它们各自的力臂,我们就得到了上面的式子,而这个式子左右两边是相等的。于是我们知道了,对于任何一个x,三个立体图形对应位置上的“切片”都能够使杠杆平衡。我们有理由相信,如果每一个切片都可以使杠杆平衡的话,取遍所有的切片后,整个系统也应该是平衡的。尽管这存在一个严密性的问题,但毫无疑问这种假设是非常合理的,并且这种想法很大程度上促成了后来微积分的产生。无论如何,Archimedes利用这种方法得到了正确的答案:假设球的体积是V,则由杠杆原理得2a*(V + π(2a)^2*2a/3) = a π(2a)^2*2a (右边那个圆柱体的重心在图形的正中间,它到支点的距离为a,这即是臂长)。解得,V=(4/3)πa^3。
Matrix67原创
做人要厚道
转贴请注明出处
欧拉的一篇研究报告:关于整数因子和的一个非常奇特规律的发现
《数学与猜想》里引用了一段欧拉的这篇经典的研究报告,写的非常精彩。你可以从中看到一个数学家是如何进行发现、归纳、猜想和论证的。你可以看到两个完全不同的数学模型里出现了惊人的巧合,通过挖掘它们之间的内在联系,最终完成了伟大的统一。
没扫描仪,拿相机拍的,效果非常不好,见谅了!
另外,拜托大家不要盗链下面的图片。









旧闻一则:神秘的0x5f3759df 不可思议的Quake III源码
Quake III公开源码后,有人在game/code/q_math.c里发现了这样一段代码。它的作用是将一个数开平方并取倒,经测试这段代码比(float)(1.0/sqrt(x))快4倍:float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
#ifndef Q3_VM
#ifdef __linux__
assert( !isnan(y) ); // bk010122 - FPE?
#endif
#endif
return y;
}
code/common/cm_trace.c中也出现了这样一段解释sqrt(x)的函数,与上面的代码唯一不同的就是这个函数返回的是number*y:/*
================
SquareRootFloat
================
*/
float SquareRootFloat(float number) {
long i;
float x, y;
const float f = 1.5F;
x = number * 0.5F;
y = number;
i = * ( long * ) &y;
i = 0x5f3759df - ( i >> 1 );
y = * ( float * ) &i;
y = y * ( f - ( x * y * y ) );
y = y * ( f - ( x * y * y ) );
return number * y;
}
这样的代码速度肯定飞快,我就不用多说了;但算法的原理是什么呢?其实说穿了也不是很神,程序首先猜测了一个接近1/sqrt(number)的值,然后两次使用牛顿迭代法进行迭代。根号a的倒数实际上就是方程1/x^2 – a = 0的一个正实根,它的导数是-2/x^3。运用牛顿迭代公式x' = x – f(x)/f'(x),式子化简为x' = x * (1.5 – 0.5a * x^2)。迭代几次后,x的值将趋于1/sqrt(a)。
但这段代码真正牛B的是那个神秘的0x5f3759df,因为0x5f3759df – (i >> 1)出人意料地接近根号y的倒数。人们都不知道这个神秘的常数是怎么来的,只能把它当作神来膜拜。这个富有传奇色彩的常数到底咋回事,很少有人说得清楚。这篇论文比较科学地解释了这个常数。