我对各种违背直觉的函数构造特别有兴趣，看看这里你就知道我对这些特殊函数有多痴迷了。因此，当我发现竟然有专门收集各种特殊函数的数学书时，可以想象我的心情有多激动。我试着以“反例”为关键字在图书馆进行检索，借了一大堆实分析数学书。这些书都已经很老了，封皮烂了又烂，已经修修补补重装了两三次封皮。翻翻这些老书，不由得对老一辈的学者和作家表示由衷的崇敬；虽然文字、排版都不出彩，但书的容量极大，内容也很实在。
废话不多说了，让我们来欣赏一下书里的一些精彩篇章吧。
微积分
随记：普遍性验证、数学思维、代数基本定理及其它
大学生活的乐趣不光体现在吃喝玩乐上，更重要的是它所提供的自由学习的场所。你可以在网上搜索课表，看看什么时候什么教室有什么牛B课，记在手机中的待办事项中，到时候到那个教室去旁听。旁听的乐趣就在于，你可以去学任何你想学的东西，不用交作业，不用怕点你名，不用记笔记，不用考试，只需要挂个耳朵在那儿听牛B东西就行了。前天一大早就被兔子叫起来，跟着一起去旁听了一节数理逻辑。
课程内容很简单，毕竟也才只讲了两周，一切都是很基础的。老师讲得很好，对联结词、命题公式、真值表等概念都说得很细致，即使完全没接触过这方面东西的人也能弄明白。作为信科的专业课，老师也简单提到了SAT问题：给定一串由AND, OR, NOT, 逻辑变量和括号组成的表达式，是否能给变量取值使得整个表达式为真？如果存在这样的“成真赋值”，我们就称表达式是一个“可满足式”。最简单的例子，p∧q就是可满足的，把p、q都取真即可；p∧(¬p)就不可满足，该式无论如何都为假。判断一个逻辑表达式是否可满足是一个经典的NPC问题，目前除了枚举之外还没有更好的算法。
还有一种逻辑表达式，不管初始值是什么，整个式子恒为真。例如，p∨(¬p)就是永真式。看起来，判定一个式子永真比判定一个式子可满足似乎要困难得多，因为前者比后者要强得多。而事实却是，这两个问题可以（在多项式的时间内）相互转化，它们在复杂程度上并无区别。如果你找到了一种可满足式判定算法，你便立即拥有了永真式判定算法。换句话说，你的算法若能找出一个成真赋值，你就能利用该算法立即得出该式所有赋值结果是否都为真。这个问题的问法很有艺术性，它有意屏蔽掉了永假式判定这一桥梁。事实上，一个表达式要么可满足要么永假，而从永假到永真只有一步之遥——只需要在最前面加一个“非”即可。也就是说，如果有一个程序，它能告诉我逻辑表达式A是否可满足，那么我就把¬A输进去：如果它说¬A不可满足，意即¬A的任何赋值结果均为假，反过来A就是永真的；如果它说¬A可以满足，意即程序找到了¬A的一个成真赋值，反过来便成为了A永真的一个反例。
数学思维游戏两则：Gabriel喇叭、世界末日论
看到新词就上一下Wikipedia确实是一个好习惯。前一篇日志的那个pdf里作者提到了Gedankenexperiment(Thought experiment)，上Wikipedia一查果然学到了牛B的新东西。好多物理定律其实完全是由思维实验推导出来的，难以置信仅仅是思考竟然就能得出物理世界遵从的各种法则。经典的物理思维实验有Newton大炮、Galileo斜塔实验、Schrödinger的猫猫、Maxwell的妖怪等等。还有，Turing机也是一个伟大的思维实验。
数学上的不少悖论（特别是涉及到维度和无穷的悖论）都是相当有趣的思维实验。Gabriel喇叭是y=1/x在[1,+∞)上的图象沿x轴旋转一周所形成的旋转体。这个简单的三维图形有一个奇特的性质：它的表面积无穷大，却只有有限的体积。为了证实这一点，只需注意到：
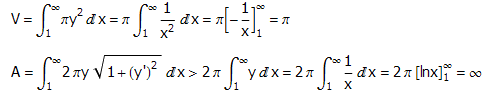
Gabriel喇叭会导出一个非常诡异的悖论：如果你想用涂料把Gabriel喇叭的表面刷一遍，你需要无穷多的涂料；然而把涂料倒进Gabriel喇叭填满整个内部空间，所需要的涂料反而是有限的。
有网友一定会问，那有没有什么二维图形，面积有限大，周长却无限长呢？答案是肯定的，Koch雪花就是这样一个经典的例子。不过，通过分形构造出来的这类图形似乎并不存在涂料悖论，因为递归到一定深度时分形图形的尺度将小于表面涂料的厚度，因此表面大小不能永无止境地算下去，涂满表面所需的涂料不再是无穷多。当考虑到涂料厚度时，原先的悖论也可以解释清楚了：填充内部空间仅仅涂满了图形的内表面，一旦考虑到涂料的厚度，它和外表面的区别就出来了。
一个与矩形剖分有关的命题（三）：诡异的微积分证明
如果一个矩形可以分割为若干个小矩形，每个小矩形都有至少一边为整数长，则原矩形同样有至少一个长度为整数的边。换句话说，用至少有一边的长度是整数的小矩形拼成一个大矩形，大矩形也有至少一条整数长的边。
在这个命题的所有常见的证明方法中，我总觉得这个证明是最诡异的。真不知道第一个想出这个证明方法的人是怎么思考出来的。把矩形放在平面直角坐标系上，左下角对齐原点(0,0)。考虑函数e^(2 · pi · i · (x+y))在每个小矩形上的积分（展开并分离变量分别积分）：
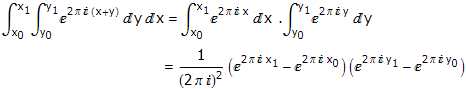
显然，这个式子等于0当且仅当(x1-x0)和(y1-y0)中至少一个是整数（也即至少有一边的长度是整数）。考虑函数在整个大矩形上的积分，它可以拆成各个小矩形上的积分的和，因此结果仍然是0。这说明，大矩形至少有一条整数长的边。
经典证明：pi^2是无理数
Proofs from THE BOOK的第六章相当精彩，这一章循序渐进地介绍了多个无理性证明。先证明e是无理数，证明方法和高数课本上的基本相同；试图用类似的办法证明e^2也是无理数时，这一章的内容开始牛B了起来，一些巧妙的变换就让原来的办法继续适用于e^2的证明；加上一些更有趣的技巧，我们还能继续证明e^4也是无理数；当证明对除0外的所有有理数r，e^r都是无理数时，全章达到了高潮。
这一章还提到了pi^2是无理数的证明方法。这个证明建立在Ivan Niven于1947年提出的“pi是无理数”的经典证明的基础上：仅仅是在原证明过程中加了一些微妙的变化就得到了pi^2也是无理数的结论。注意到，“pi^2是无理数”是一个比“pi是无理数”更强的结论。由于有理数的平方还是有理数，因此证到了pi^2是无理数也就说明了pi必然是无理数；但反过来却不行，因为无理数的平方不一定也是无理数，比如根号2的平方就不是无理数。
证明过程用到了一个函数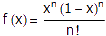
，其中n是一个任取的大于等于1的常数。可以想像，这个函数的分子部分展开后是一个关于x的整系数多项式，最低次数为n，最高次数为2n。我们将用到这个函数的两个性质：首先，当0<x<1时，显然有0 < f(x) < 1/n!；其次，函数f及其任意阶导数在x=0和x=1处都是整数。为了证明后一个结论，首先注意到当x=0时，不管是多少阶的导数，除了常数项以外其余项都是0；常数项只可能在n<=k<=2n时出现（k表示k阶导数），但此时它等于一个整系数乘以k!/n!，显然也是个整数。另外，由于f(x)=f(1-x)，根据复合函数的微分法我们立即得到
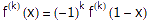对任意x都成立，当然也就有
。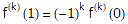