显然,过 Pizza 的圆心作四条直线,把一个周角平分成八等份,则整个 Pizza 饼也被分成了八等份。我们也很容易联想到,如果过圆心外的一点做出四条直线,并且同样满足每两条相邻直线夹 45 度角,那么这八块 Pizza 饼显然是不一样大的。考验你直觉的时候到了:你认为蓝色面积之和与红色面积之和相比,哪个大一些呢?
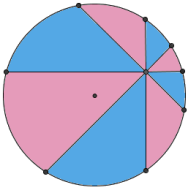
显然,过 Pizza 的圆心作四条直线,把一个周角平分成八等份,则整个 Pizza 饼也被分成了八等份。我们也很容易联想到,如果过圆心外的一点做出四条直线,并且同样满足每两条相邻直线夹 45 度角,那么这八块 Pizza 饼显然是不一样大的。考验你直觉的时候到了:你认为蓝色面积之和与红色面积之和相比,哪个大一些呢?

在处理最优化问题时,我们常常通过分析导函数来寻找极值点,因此往往希望目标函数是可导的;但在很多实际问题中,目标函数里经常带有取最大值函数,它的存在将破坏函数的可导性。一个有趣的问题由此产生:能否设计一个平滑的二元函数 f(x,y) ,它的效果近似于 max(x,y) ,足以用来代替最大值函数?在设计这样的函数时,下面这些条件需要尽可能满足:
· 函数简洁而美观
· 可以调整函数的“平滑度”
· 可以很方便地扩展到多个变量
在今天晚上的微观经济学课上,我又听到了一个比较有意思的东西。试着找找各种类型的连续函数f(x),画出f'(x)和f(x)/x的函数图像,你会发现一个奇怪的现象:f'(x)与f(x)/x相交的地方都是f(x)/x取到极值的地方。简单地算一算,我们不难证实这个结论。f(x)/x的导数等于f'(x)/x – f(x)/x^2。将f'(x)=f(x)/x代入上式,可得f'(x)/x – f(x)/x^2 = f(x)/x^2 – f(x)/x^2 = 0。这就是说,当f'(x)与f(x)/x相等的时候,f(x)/x的导数一定等于0。有意思的是,这个结论还有一个非常直观的解释,你能想到吗?
最近几天见到了几道零散的、不成系统的趣题,在这里合成一篇文章,与大家分享。
1. 证明:对任意正整数n,n^2+n+1一定不是完全平方数。
2. 说一个实数是可表达的,当且仅当它能用有限长的语句明确地描述出来,如2147483648可以说成是“二的三十一次方”,√2即为“平方后等于二的正实数”,π即为“圆的周长和直径之比”。问题是,是否存在一个不可表达的实数?
3. 一个人有两个小孩儿,其中有一个生于星期二的男孩儿。问另一个是男孩儿的概率是多少?
4. 无需积分,计算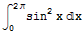 。
。