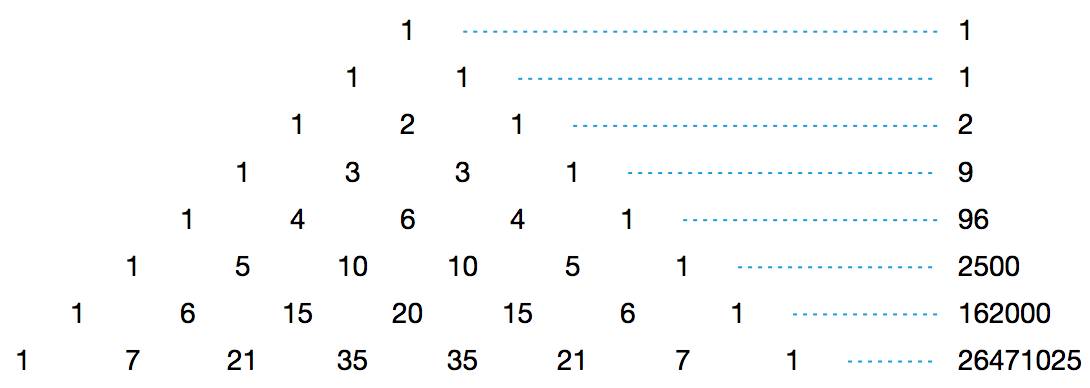
你相信吗,杨辉三角里竟然也有自然底数 e 的身影。 2012 年, Harlan Brothers 发现了杨辉三角中的一个有趣的事实。不妨把杨辉三角第 n 行的所有数之积记作 sn ,那么随着 n 的增加, sn · sn+2 / sn+12 会越来越接近 e ≈ 2.718 。事实上,我们有:
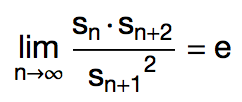
这是为什么呢? John Baez 在这个网页上给出了一个漂亮的解释。

你相信吗,杨辉三角里竟然也有自然底数 e 的身影。 2012 年, Harlan Brothers 发现了杨辉三角中的一个有趣的事实。不妨把杨辉三角第 n 行的所有数之积记作 sn ,那么随着 n 的增加, sn · sn+2 / sn+12 会越来越接近 e ≈ 2.718 。事实上,我们有:
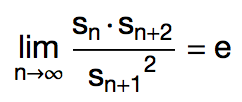
这是为什么呢? John Baez 在这个网页上给出了一个漂亮的解释。
Heron 公式是一个已知三角形三边长便能直接求出其面积的经典公式。把三角形的三边长分别记作 a 、 b 、 c ,令三角形的半周长 p = (a + b + c) / 2 ,则三角形的面积可以用 Heron 公式 S = √p(p – a)(p – b)(p – c) 求出。如果把 p = (a + b + c) / 2 代入式子,得到的公式其实也挺对称的: S = √(a + b + c)(a + b – c)(a – b + c)(- a + b + c) / 4 。
现在,我们把这个公式看作是一个关于 c 的函数: f(c) = √(a + b + c)(a + b – c)(a – b + c)(- a + b + c) / 4 。它的导数是多少?
注意到,利用平方差公式,根号内的式子可以进一步整理为 ((a + b)2 – c2)(c2 – (a – b)2) ,它的导数是 – 2c(c2 – (a – b)2) + 2c((a + b)2 – c2) = 4c(a2 + b2 – c2) 。因而,整个原函数的导数就是 c(a2 + b2 – c2) / (2 · √(a + b + c)(a + b – c)(a – b + c)(- a + b + c) ) 。
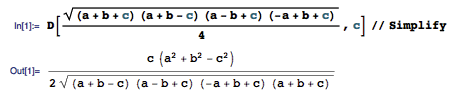
有趣的是,当 a 、 b 、 c 满足勾股定理的关系 a2 + b2 = c2 时,导数值正好为 0 。这是为什么? Heron 公式的导数的零点和勾股定理有什么联系呢?
曾经想过要写一篇科幻小说,讲一种生活在空壳星球内表面的文明,如何发现自己的星球是圆的,如何成功地环游世界一周,又如何发现自己其实是在星球的内表面。今天我长出了一口气,幸好当初没写这样的文章,不然就闹笑话了。今天我才知道,空壳星球内部的人是不能居住在星球的内表面的,因为空壳星球内的任意一点都没有重力。
这其实并不难理解。虽然脚下的土地离你更近,产生的重力作用更显著,但可惜这部分土地并不多。星球的更多部分将会位于你的头上,但可惜它们又离你太远了,影响也不会太大。近的部分太小,大的部分又太远,这两者很可能是一种平衡的状态。
公式 h = (1/2)·g·t^2 里, t 头上的平方并不奇怪。显然,物体下落的路程是与重力加速度 g 和时间 t 有关的,高度 h 就由这两个变量决定。注意到 g 是一个加速度单位,是米除以平方秒的形式;为了得出一个以长度为单位的结果,我们必须要消除分母位置上的“平方秒”,因而时间变量 t 必须要以平方的形式出现。
类似地, E = m·c^2 里的平方也不是凭空而来的。能量的单位是牛乘以米,牛本身又是千克乘以米每平方秒,刨根到底能量的单位就该是 千克·(米^2)/(秒^2) ,正好符合等式右侧“质量乘以速度平方”的量纲。
在数学中,量纲法也是无处不在。 n 维球的体积公式一定是半径的 n 次方乘以一个系数, Heron 公式 A = √s(s – a)(s – b)(s – c) 看似复杂的外表下也遵循着量纲这一金科玉律。给定 n 个数,我们有多种定义其平均数的方案,包括所有数之和的 n 分之一(算术平均数),所有数乘积的 n 次方根(几何平均数),所有数的倒数和的倒数的 n 倍(调和平均数),所有数的平方和的 n 分之一的平方根(均方根),等等。由于一组数的平均值的量纲应该和这些数本身的量纲保持一致,因此在各种平均数的公式里,平方了就要开回去,取倒了还得倒回来,全乘在一起就得开 n 次方,这样才能得到同样类型的数。
自从在《怎样解题》里看到了量纲法,在学习和讲解数理知识时我便特别留意量纲,慢慢总结出上面这些用于说明量纲规律的经典例子。今天,我又看到了一个把量纲用得神乎其技的经典例子,在这里和大家分享。