The Bottle Imp 是一则有意思的短篇小说。某日，小说里的主人公遇上了一个怪老头。怪老头拿出一个瓶子，说你可以买走这个瓶子，瓶子里的妖怪就能满足你的各种愿望；但同时，持有这个瓶子会让你死后入地狱永受炼狱之苦，唯一的解法就是把这个瓶子以一个更低的价格卖给别人。如果你是小说里的主人公，你会不会买下这个瓶子呢？你会以什么价格买下这个瓶子呢？
    以什么价格买入这个瓶子，这个问题貌似并不容易回答。你当然不愿意花太多的钱，在你的愿望被满足之前你至少还得给自己留一点钱花；但你也不能花太少的钱，否则你会承担着卖不出去的风险。但是，在做出一些理性的分析后，我们得出了一个惊人的结论：任何人都不应该以任何价格购买这个瓶子。
    和很多博弈问题一样，这一系列的分析首先从最简单的情形开始。首先，你是绝对不能只出 1 分钱就买下这个瓶子的，因为这样的话这个瓶子就永远也卖不出去了——没有比 1 分钱更低的金额了。那么，用 2 分钱买瓶子呢？这样理论上貌似是可行的，但仔细一推敲你会发现还是有问题——这样你只能以 1 分钱卖掉这个瓶子，但没有人会愿意用 1 分钱去买瓶子（否则他就卖不掉了）。因此，用 2 分钱买下瓶子后，你同样找不到下一个买家。和上面的推理一样，用 3 分钱买这个瓶子也不是什么好主意，因为没有人愿意以 1 分钱或 2 分钱购入瓶子，因此你的瓶子不可能卖得掉。依此类推，你不应该以任何价钱去购买这个瓶子，因为每个人都知道，他无法以任何价格卖掉这个瓶子。

Read more…

    我没有接菜单。“六成熟的牛排加一份炸鳕鱼，谢谢”，我说。穿着艳丽的服务员MM拿着菜单微笑着退下。下午四点起床的好处在于，在任何一家餐厅就餐都不会有太多的人；不好的就是，没有人会陪你来吃。一个人在餐厅用餐看上去多少有些滑稽。
    我把视线移到桌子对面的那个人。他手中翻开的《科幻世界》正好遮住了他的脸。从封面来看这应该是最近的一期，几个非常不起眼的五环标志和与背景几乎融为一色的中国字暗示着这期《科幻世界》的封面展示的是未来某次在中国举办的奥运会的盛况。我正想说“你也喜欢《科幻世界》么”时，他先发话了：“兄弟，你点的东西和我刚才点的完全一样。”他放下手中的杂志，我俩四目相对。我惊呆了。面前的这个人体型和我别无二致，穿着和我一样的衣服，留着完全相同的发型和胡子，脸上的斑点仿佛是用一个模子印出来的。如果不是他手中比我多拿了一本杂志，我可能会真的以为我面对的是一面镜子。
    我静下心来，说道：“这让我想起了Kiefer Sutherland的新电影……”
    话没说完，他接了一句“Mirrors吧，镜子里的人和镜子前的人动作不一样……”
    他提到国外电影时也直接用英文名，这让我很是吃惊。我说：“但这部电影绝对比不上Kiefer Sutherland的另一经典之作。”
    “你说Dark City吧，经典中的经典了。”他条件反射式地回答到。这绝对不是巧合！电影Dark City的知名度远远小于Kiefer Sutherland出演的火热美剧24。我本以为他会回答24的，但他给出的答案和我预想的完全一致。
    他也开始试探性地发问：“你知道吗，最近Dark City出了一个特别的……”
    我就知道他要说这个。我连忙抢过话头：“……10周年导演剪切版。哈哈，我还真想再看一次！”
    “对啊，因为这个导演剪切版改了很多，网上有人甚至评论说‘就像变成了另一部电影’。”
    “难道……”我长大了嘴，指着他惊奇地叫到，“难道你也经常去digg上看新闻？”
    “呵呵，我还经常去found四个f呢！”
    我笑了，“他妈的四个f，我他妈的还去八个i呢……”
    “怎么你也……”他的声音明显地变了调。然后我们沉默了。网络中的语言在日常口语交际中的频频出现给这种沉默带来一些轻微的喜剧效果。

Read more…

    前两篇文章中，我们提到了两个用杠杆原理解决数学问题的例子。这篇文章将从另一个物理领域出发，探索光学的一个重要原理与几何极值问题的关系。
    物理学的美不仅仅表现在简洁的公式上。我们还惊奇地发现，很多物理现象都是按照使某个变量达到极值的方式发生。一个典型的例子就是Fermat原理，它指出了光的传播路径的一个重要规律：光总是沿着所花时间最短的路径传播。这里我们将简单介绍一下Fermat原理，该系列后面的文章里将会用到这一原理。
    Fermat原理俗称“最快到达原理”、“最小时间原理”，意思是光线传播的路径总是满足这样一个规律：它总能使光在最短的时间内到达目的地。这个原理完美地统一了直线传播定律、反射定律和Snell定律，解释了为什么光线总是沿直线传播，为什么入射角等于反射角，以及光线在不同介质间传播为什么会发生折射现象。
    在Ted Chiang的著名科幻小说The Story of Your Life里有这样一段形象的描述：

    “好，这是一条光线从空气射进水中所走的路线。在碰到水面前，光线沿着直线前进；水有不同的折射率，所以光改变了前进方向。你以前听过这个，对吗？”
    我点点头，“当然。”
    “现在关于光所走路线有个有趣的性质。这条路线是这两点之间可能的最快的路线。”
    “又来了？”
    “想象一下，光线沿着这条路线前进。”他在图解中加了条虚线。
    “这条假想中的路线比光实际走的路线要短。但是光在水中前进的速度比在空气中小，而这条假想的路线的很大一部分是在水中的，所以光沿着这条假想的路线所花的时间要比沿着实际路线要长。”
    “好，我明白了。”
    “现在想象一下，假设光沿和另一条路线前进。”他画了第二条虚线。
    “这条路线减少了在水中的比例，但总长增加了。光沿着这条假想的路线所花的时间也要比沿着实际路线要长。”
    Gary放下粉笔，用蘸着粉笔屑的手指指着黑板上的图解，“任何假想的路线都比实际的要花更多的时间。换一句话说，光线走的路线是最有可能走得走快的一条。这就是Fermat定理的最小时间原理。”

    你发现Fermat原理有什么奇怪的地方了吗？你是不是感觉Fermat原理很诡异，但自己也说不清楚到底是为什么诡异？仔细想想你会发现，“最快到达”这种原理显然是不符合我们的行为方式的：假如我是光，我的传播规律是“最快到达”，但此时我要传播到哪里还不知道呢。Ted Chiang的小说对此也做出了详细的描述：

    “然而我仍要问你关于Fermat定理的东西。它的一些东西让我感到奇怪，但我不能正确指出那是什么。它只是不像是物理法则。”
     Gary的眼睛闪了一下，“我打赌我知道你想谈什么，”他用筷子把锅贴夹成两半，“你习惯于用起因和结果来思考折射：光照到水面上是起因，方向的变化是结果。但Fermat定理听上去很古怪，因为它以目的的形式来描述光的行为。它就像是光线的指挥官，‘你应该将抵达目的的时间最小化或最大化。’”
    我想了一下，“继续说。”
    “这是物理法则的一个老问题。人们在17世纪Fermat定理第一次成形时就一直在谈论它。Planck写了好几卷。本质是，普通的物理法则的表述是具有因果关系的，而像Fermat定理的可变法则具有目的性，几乎是目的论。”
    “嗯，这样解释道挺有趣。让我想一下。”我拿起一支标签笔，在餐巾纸上画了幅图解，就是Gary在我的黑板上画的那幅，“好，”我想我很大声地说道，“那么让我们假设光的目的是要沿着最快的路线前进。这样的话，光如何走呢？”
    “好吧，假若按人类行为学来说，光得检验每条可能的路线并计算每条得花多少时间。”他从盘子里戳起最后一块锅贴。
    “那样做的话，”我继续道，“光线得知道目的在哪儿。假如目的地在某某其他地方，最快的路线就会不同。”
    Gary再次点点头，“完全正确。‘最快的路线’的概念是无意义的，除非有特定的目的地。计算沿着一条假想的路线需多长时间也需要关于在这条路线上有什么东西的信息，比如水面在哪？”
    我继续看着纸巾上的图解，“在光开始移动前，它得事先知道所有这一切，对吗？”
    “这样说来，”Gary说，“光线不能沿着老路前进，然后再在后来返回。因为引起这样行为的路线不是最快的。在一开始光就已经做好了全部的计算。”
    我心中暗想，在光线能够选择它移动的方向前，它已经知道它最终会在那里结束。我知道这让我想起了什么，我抬起头看着Gary，“这让我困扰。”

  
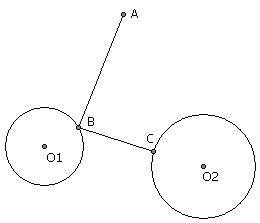
    上面的论述似乎很抽象。我们来看一个实际的数学问题。这个问题有点怪，和其它的问题很不一样。给出一个点A，给出两个圆O1、O2，再给定O1上的一点B，问O2上是否存在一点C，使得B点的位置恰好能让AB+BC达到最小，也即对于O1上异于B的任一点B'都有AB'+B'C > AB+BC。你一时间可能找不到这个点C，这很正常，但光可以立即找到这个点C。因为从Fermat原理的角度看，光的思维方式是“逆向”的，这个别扭的题目正好顺应了它的思维方式。只要沿AB发射一条光线，在圆O1表面上发生反射后的光线与O2的交点即为点C。因为，A->B->C这条光路符合光的传播性质，这条路径是所有经过O1上一点到C的路径中最短的一条，其它所有的B'都会使光程增加。事实上，光就有这种神奇的本领：不管之前有过多少反射点，有过多少折射点，这条光线今后传播到的每一个点都满足这种无比别扭的“以它为终点则前面的定点均已达到最优”的性质。对于光来说，这是顺理成章的事；但从我们的角度来看，还没到目的地便能确保路径最优是很不可思议的。我们会习惯性地认为，光从A点出发往B走之前必须得先知道它的终点是C，然后才会知道B可以使光程最短，因此它才会往B走。这是明显有悖于我们熟知的因果关系的。或许说，这个世界本没有什么因果关系，仅仅是因为人类的思维被禁锢在了因果链式思维中？

    接下来，我们举两个火星例子。两个都是经典的小学奥赛题。
  
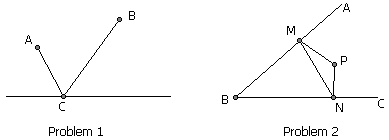
    问题1：给定直线l同侧的两点A和B，在直线上找一点C使得折线ACB最短。
    问题2：角ABC内有一点P，请在AB上找一点M，BC上找一点N，使得三角形PMN的周长最短。
    类似的问题还有很多。很多这类几何极值问题都和Fermat原理有直接

    今年恰逢PKU数学文化节十周年，其间开办的很多讲座我都去了。去听讲座的人好像都是数院的，我恐怕是唯一一个中文系的。考虑到我和中文系的MM没有共同话题，因此每一次听讲座时我都会顺便四处打望，看看有没有数院的美女，下来可以和她“交谈”一下。有趣的是我的做法与常人所想的恰好相反：据说数院的已经盯上中文系的MM了，而我一个中文系的竟然反过来去找数院的MM。
    昨天有一个关于非欧几何的讲座，这是目前所有的讲座中最为精彩的一次。讲座里提到了Poincaré的一个双曲几何模型，感觉非常有意思，在这里和大家分享一下。
    在所有的双曲几何模型中，Poincaré的圆盘模型可能是最有趣的一个。这个双曲世界存在于一个有限的平面区域里，整个世界限制在一个单位圆的范围内。这个世界中有两个最重要的物理定律：一，假如某物体X离原点O距离为d，那么该物体的温度为1-d^2；二，物体的大小与温度成正比。这样，假如某个人从这个世界的中心走向边缘，那么他的温度会从1慢慢变成0，同时整个人慢慢变小。他自身大小改变的同时周围的物体也等比例地放大或缩小，而这个世界里的人视野有限，看不见远处的东西，因此他不会觉得自己变小了或者变大了。因此，在这个世界里，物理学家们能够很轻易地发现第一定律，但要发现第二定律则非常具有挑战性，探索第二定律的过程必然很曲折，并且很可能出现哥白尼时代的故事。
    对于我们来说，这个世界是有界的；但对于这个世界中的人来说，这个世界是无穷大的。因为离原点越远，人就越小，于是相对来说他们所看到的空间也就越大。当人的位置趋于边界时，物体大小趋于0，此时的空间将变得无穷大，因此这个世界中的物体永远无法到达边界。同时，离原点越远的话越接近“绝对零度”，这将非常不适宜生物的生存，因此人们大多居住在原点，离原点越远城市规模越小，更远的地方则完全没有开发过，只适合于疯狂的冒险家进行极限运动。于是这个世界中的物理学家很自然地得到这个结论：世界是无穷大的。
    下面就神奇了。现在，考虑某个人想从A点走到B点。如果按照红色的线段直直地走过去，所走的路程并不是最短的，因为这条路线离原点较远。聪明的人会发现，我先往原点方向走一点，然后再到B点去，这样走的路程更短一些。我们猜想，最短路线很可能是一条偏向于原点的弧线（就好像原点把直线段“吸”过去了一样）。之所以产生这种奇怪的现象是因为，离原点越远物体就越小，人的步子也变小了，相对来说实际空间就变大了。因此，对我们来说距离相等的两点，对他们来说离原点越远其实际距离越大。因此，我们有必要重新定义这个双曲世界中“距离”的概念。由于物体大小与1-d^2成正比，因此我们可以定义，如果在离原点距离为d的位置上有一个充分小的位移，在我们看来距离为Δx，那么在这个世界中的实际距离就是Δx/(1-d^2)。这样就可以算出，从A到B的最近路线是一条垂直于边界的圆弧（蓝色的那条）。于是在这个世界中，“直线段”已经不再是我们熟悉的直线段了，而是一条条的弧线（还包括整个圆的直径）。而我们眼中的直线，在他们看来就是曲线。
      
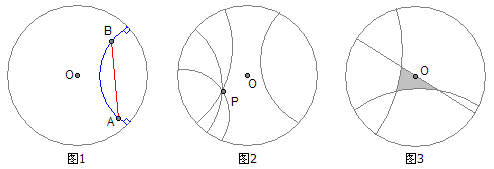
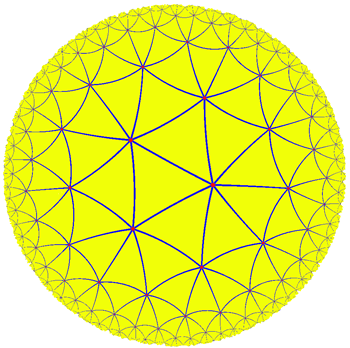
    这个世界中的几何满足欧式几何的前面四个公设，但不满足第五公设。比如，两点确定一条直线，因为过两点的圆弧只有一条垂直于这个世界的边界；而直线可以无限延长，因为离边界越近两点的实际距离越大，你永远走不到尽头。但是，这个世界不满足第五公设。从图2可以看到，过一点可以作无数条直线不与已知直线相交；从图3可以看到，三角形的内角和小于180度。下面这幅图片可以帮助你更好地理解这个双曲模型。这是该平面上的一个三角形剖分，里面的所有三角形都是等边三角形，而且所有这些三角形都是一样大的。你可以看到7个等边三角形共用一个顶点，这说明三角形的内角和小于180度。

    另外值得一提的是，这个构想很适合写成一篇科幻小说。记得大刘的那篇科幻吗？一群电子器件诞生在某颗星球的内核，然后探索物理定律，历经重重困难，最终冲破了它们那个世界的“天然外壳”，看到了外面的世界，并相信我们整个宇宙也处于一个更大的星体内。这个双曲几何模型也很适合写出这样的小说来，比如以物理史书的方式叙述从古至今若干个传奇人物的故事，讲述他们是如何从一些奇怪的现象出发，通过各种试验证明自己的猜想，顶住社会各方面的压力，执著地探索宇宙的奥秘。小说中的人物可以带着读者一起进行探索，最后才告诉读者这个宇宙的本质是什么。

Matrix67原创
转贴请注明出处

    Flatland是一部巨经典的科学幻想小说，小说里构造了一个全新的世界──这个世界是二维的！整个小说分成两个部分，前一部分系统地描述这个二维世界，包括自然状况、居民生活、政治历史等等。真正有趣的事情发生在后一部分里，这里不同维度的世界之间发生了碰撞——二维世界中的主人公拜访了一维世界，同时又接触到了一个全新的三维世界。当他在他的世界传播三维思想时，整个世界大乱，哥白尼时代的那段故事再次发生。
    Flatland: The Movie是由此改编的一个动画短片，整个电影大约30分钟。官方网站上已经放出了电影的预告片，看起来非常有意思：

下面是一个两分多钟的片段：

原版小说：http://xahlee.org/flatland/index.html
陈忱译《神奇的二维国》：http://www.matrix67.com/data/flatland.html
官方网站：http://flatlandthemovie.com/
imdb链接：http://www.imdb.com/title/tt0814106/

现在，你可以在官方网站上订购学校教育专用的特别版DVD，价格是120美元；30美元的个人版DVD还要过几个月才能订购。