曾经看到过自动扫雷软件，当时我就在想，扫雷游戏是否有什么牛B的多项式算法。最近才看到，扫雷问题居然是一个NP完全问题，并且这个定理有一个简单、直观而又神奇的证明。在这里和大家分享一下整个证明过程。
    首先，扫雷一定是NP问题，它显然可以在多项式的时间里验证一个解。接下来，我们需要把一个已知的NP完全问题归约到扫雷问题上去。我们将给出一种把逻辑电路问题归约到扫雷问题的方法，这样的话我们就可以利用扫雷问题解决逻辑电路问题，从而说明逻辑电路问题不比扫雷难。我们将把逻辑电路问题转换成一种对应的扫雷布局，就像画画一样把逻辑电路画在扫雷的棋盘上。如果你还不知道什么叫NP完全问题，什么叫逻辑电路问题，你可以看一看我的这篇文章。

   
    上图就是一条带有Boolean值的线路。注意到x和x’中有且仅有一个有雷。如果（沿线路方向）前一个格子有雷，我们就说这条线路状态为True；反之如果后一个格子有雷，那么这条线路所传递的Boolean值就是False。每条线路的起始端都如下图左所示，其中符号*表示该格里必然有雷，x和x’中同样是有且仅有一个有雷，但到底是哪一个里面有雷谁也说不清楚。线路是可以拐弯的，如下图右所示，这可以保证转角后Boolean值相同。
   

Read more…

    在这篇文章里，我们从信息论的角度证明了，基于比较的排序算法需要的比较次数（在最坏情况下）至少为log2(n!)，而log(n!)=Θ(nlogn)，这给出了比较排序的一个下界。但那里我们讨论的只是最理想的情况。一个事件本身所含的信息量是有大小之分的。看到这篇文章之后，我的思路突然开阔了不少：信息论是非常强大的，它并不只是一个用来分析理论最优决策的工具。从信息论的角度来分析算法效率是一件很有趣的事，它给我们分析排序算法带来了一种新的思路。

    假如你手里有一枚硬币。你希望通过抛掷硬币的方法来决定今天晚上干什么，正面上网反面看电影。投掷硬币所产生的结果将给你带来一些“信息”，这些信息的多少就叫做“信息量”。如果这个硬币是“公正”的，正面和反面出现的概率一样，那么投掷硬币后不管结果咋样，你都获得了1 bit的信息量。如果你事先就已经知道这个硬币并不是均匀的，比如出现正面的概率本来就要大得多，这时我们就说事件结果的不确定性比刚才更小。如果投掷出来你发现硬币果然是正面朝上，这时你得到的信息量就相对更小（小于1 bit）；反之如果投掷出来居然反面朝上了，那你就得到了一个相对较大的信息量（大于1 bit）。但平均下来，我们得到的信息量是小于1 bit的，因为前者发生的可能性毕竟要大一些。最极端的情况就是，这是一枚被捣了鬼的魔术硬币，你怎么投都是正面。此时，你投了硬币等于没投，反正结果都是正面朝上，你得到的信息量永远为0。
    这个理论是很符合生活实际的。昨天晚上我出去吃饭时，坐在我后面的那个人是男的还是女的？这种问题就比较有价值，因为大家都猜不到答案究竟是什么；但要问我昨天跟谁一起出去上自习去了，问题的答案所含的信息量就变小了，因为大家都知道如果我破天荒地跑去自习了的话多半是有MM陪着一起去的。如果有网友问我是男的还是女的，那就更不可思议了，因为我不但多次在这个Blog里提到我一直想找一个合适的MM，还在AboutMe里面发了我的照片。如果某人刚操完一个MM，突然扭过头去问“对了，你是男的还是女的呀”，那这个人绝对是一个不折不扣的大傻B，因为这个问题所能带来的信息量几乎为0。
    总之，当每种结果出现的概率都相等，事件的不确定性达到最大，其结果最难预测时，事件的发生将会给我们带来最大的信息量。我们把一个事件的不确定程度叫做“熵”，熵越大表明这个事件的结果越难以预测，同时事件的发生将给我们带来越多的信息。如果在排序算法里每次比较的熵都是最大的，理论上来说这种（基于比较的）排序算法就应当是最优的。但我们一会儿将看到，我们已知的排序算法总是不完美的，每种算法都会或多或少地存在一些价值明显不大的比较。

Read more…

图片来源：http://xkcd.com/399/
号外：期待了9个多月的PSP游戏Echochrome已经发行，网上到处有下载

  
    有这样的一类组合游戏，对于任一个游戏局面，游戏双方的合法决策都完全一样，游戏对战双方的唯一区别就是看谁先走。这样的游戏叫做Impartial Games。像什么报数啊，取火柴啊，取石子啊，这些游戏都属于Impartial Games；而象棋、围棋等要分棋子颜色的游戏则不属于Impartial Games。共享状态的游戏几乎没有可玩性，因为游戏开始前我们就能知道谁赢谁输（如果双方均使用最佳策略）。棋局的任一状态只有两种，面对这个棋局的人要么必胜要么必败。考虑这样的一个递推关系：如果一个状态是必胜态，那至少有一种走法能走成一个必败态留给对方；如果一个状态是必败态，那它怎么走都只能走到必胜态。运用这样的关系，我们可以自底向上推出初始状态是必胜还是必败。
    近来有人提出一个名为Atropos的游戏，它就是一个即使计算机也很难办的Impartial Game，它能保证这个游戏仍然具有可玩性。游戏在一个Sperner三角形上进行，上图就是一个边长为7的Sperner三角形。游戏开始后，双方依次在白色的圆圈里涂上红色、绿色或者蓝色，已经涂过颜色的圆圈不能再涂色。另外，只要有可能，所涂的圆圈都必须紧挨着上次对方涂的那个圆圈。谁先涂出三种颜色都有的小三角形，谁就输掉这场游戏。

  
    注意这个游戏是不可能出现平局的。当所有白色圆圈全部涂上了颜色后，至少会出现一个红绿蓝小三角形。为了证明这一点，我们可以在所有的绿色和红色圆圈中间画一个箭头，红的在箭头右边，绿的在箭头左边。这些箭头一定组成了一条一条的路径，它们既不会交汇也不会分岔。但整个图的边界上进来的箭头有4个，出去的箭头只有3个，于是至少有一条路径在里面走死了，也即迎面碰上了蓝色的圆圈。这样，我们就找到了一个红绿蓝三色都有的小三角形。

    这个游戏虽然属于Impartial Games，但它仍然具有可玩性。从直觉上看，这个游戏中的先手后手几乎没有区别，谁也不占优势。这篇论文则严格证明了，判断Atropos游戏的最佳策略属于PSPACE-complete，这是所有使用多项式空间的问题中最难的一类，所有使用多项式空间的问题都可以（在多项式的时间内）约化到它。这说明，Atropos游戏没有什么很显然的“决窍”，即使利用计算机也很难确定最优决策。

在线游戏：http://cs-people.bu.edu/paithan/spernerGame/SpernerGame.html (Java Applet)
查看更多：http://cs-people.bu.edu/paithan/spernerGame/

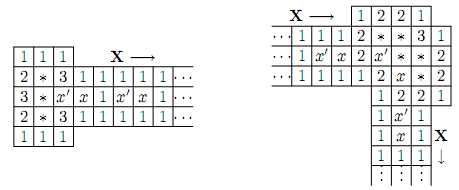
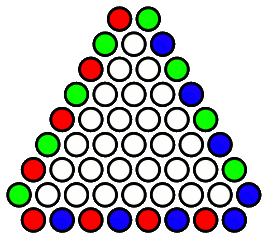
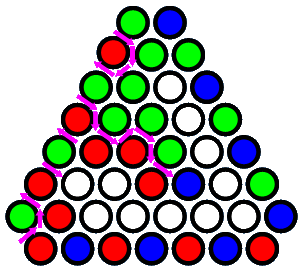
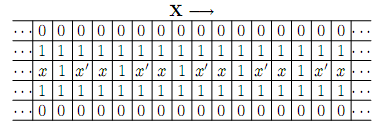    SETI@home可以在杂乱的射电数据中搜寻独特的讯号，你能在大街上的嘈杂声中清晰分辨出一个尖细的女声大叫“亚美蝶”。这些现象都表明，有时对集合里的所有元素进行整体考察可以很快找出我们所要找的个体。去年我们搞合唱比赛时，我又想到了一个绝佳的例子：你可以在合唱声中清楚地听到是否有人跑调。考虑这样一个问题，假如合唱团里有一个人唱歌始终走调，但我听不出来是谁走调，只能听出当前正在唱歌的人中是否有唱走调了的人。那么，我如何才能迅速地揪出那个唱走调的人？利用经典二分法，我们可以在log2(n)次合唱后找出唱走调了的人。每一次，我都把剩下的人平均分成两组，然后选其中一组来合唱：如果听不到走调的声音，这一组的人就全部过关；如果听到有人走调，那另一组里的人都可以被排除了。递归地对剩下的组进行同样的操作，log2(n)次操作后必定可以找出那个唱歌走调的人。
    现在的问题变得有些麻烦了。假如我们知道合唱队里有一个人唱歌爱跑调，但他不是总会跑调。具体地说，他只有1/2的概率唱错，但其余1/2的时间里他却唱得很准。现在，传统的二分法不再适用了，因为没有走调声已经不能起到排除的作用了。你能想出多少种可行的算法来找出那个人？下面提出一些可行的方法，你认为哪种方法更好？你能求出这些算法所需要的检测次数的期望值各是多少吗？

    1. 不断地随机生成一个大小为n/2的子集并对其进行检测，直到某次不能通过检测为止，然后递归地对其进行操作。
    2. 所选的子集大小为n/2是最优的吗？把上面这种方法的n/2改成n/a，常数a的最优值是多少？
    3. 检测次数的期望值还可以更小吗？我们想到，每次都重新生成一个新的集合其实并不科学，新集合本身是否包含老鼠屎也是得碰碰运气的。因此，对方法1的一个合理改进是：把集合平均划分为两个部分，交替对它们进行检测直到某次检测没通过为止，然后对该组递归操作下去。这种方法真的比前两种好吗？它所需要的期望次数是多少？
    4. 尝试对方法3进行改进。如果把集合平均划分成3份并循环进行检测，效果会不会更好一些？

    1. 选取的子集有1/2的概率覆盖了我们要找的那个人，子集里有他而他这次恰好又唱走调了则有1/4的概率。因此，不管规模有多大，平均需要4次才能把规模缩小一半。因此，检测次数的期望值为4*log2(n)。为了方便比较期望值的大小，后面的答案我们一律表示成一个常数乘以log2(n)的形式。
    2. 类似地，平均需要2a次检测才能把规模缩小到原来的1/a，因此总共花费的检测次数为2a*log2(n)/log2(a)。对函数求导，可得当a为e时函数值达到最小。此时的检测次数期望值为2e*log2(n)/log2(e)≈3.7683 * log2(n)。
    3. 这个就经典了。设方法3里把规模缩小一半所需要的检测的期望次数为m，下面我们来看m应该等于多少。把n个人平均分成两组，我们要找的老鼠屎有1/2的概率在第一组，有1/2的概率在第二组。因此，第一次就测出问题来有1/4的可能，第二次就测出问题也有1/4的可能。对于剩下的1/2种情况，局面变得又和最开始一样，只是平均需要的检测次数比原来多了2。根据期望值的定义，有m=(1/4)*1 + (1/4)*2 + (1/2)*(m+2)，解得m=3.5。总的检测次数就是3.5 * log2(n)，它比前面两种方法都要好。你可能不同意上面求m的方法。这没啥，如果你不断对m进行迭代，你会发现展开出来的式子就是最标准的期望值定义。
    4. 类似地，有m=(1/6)*1 + (1/6)*2 + (1/6)*3 + (1/2)*(m+3)，解得m=5。于是，把规模缩小到原来的1/3平均需要5次检测，总的检测次数为5*log2(n)/log2(3)≈3.1546 * log2(n)。

题目来源：IBM Ponder This Dec07
原文还从熵的角度探寻了问题的最优算法，感兴趣的读者可以去看一看