Proofs from THE BOOK的第六章相当精彩,这一章循序渐进地介绍了多个无理性证明。先证明e是无理数,证明方法和高数课本上的基本相同;试图用类似的办法证明e^2也是无理数时,这一章的内容开始牛B了起来,一些巧妙的变换就让原来的办法继续适用于e^2的证明;加上一些更有趣的技巧,我们还能继续证明e^4也是无理数;当证明对除0外的所有有理数r,e^r都是无理数时,全章达到了高潮。
这一章还提到了pi^2是无理数的证明方法。这个证明建立在Ivan Niven于1947年提出的“pi是无理数”的经典证明的基础上:仅仅是在原证明过程中加了一些微妙的变化就得到了pi^2也是无理数的结论。注意到,“pi^2是无理数”是一个比“pi是无理数”更强的结论。由于有理数的平方还是有理数,因此证到了pi^2是无理数也就说明了pi必然是无理数;但反过来却不行,因为无理数的平方不一定也是无理数,比如根号2的平方就不是无理数。
证明过程用到了一个函数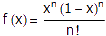 ,其中n是一个任取的大于等于1的常数。可以想像,这个函数的分子部分展开后是一个关于x的整系数多项式,最低次数为n,最高次数为2n。我们将用到这个函数的两个性质:首先,当0<x<1时,显然有0 < f(x) < 1/n!;其次,函数f及其任意阶导数在x=0和x=1处都是整数。为了证明后一个结论,首先注意到当x=0时,不管是多少阶的导数,除了常数项以外其余项都是0;常数项只可能在n<=k<=2n时出现(k表示k阶导数),但此时它等于一个整系数乘以k!/n!,显然也是个整数。另外,由于f(x)=f(1-x),根据复合函数的微分法我们立即得到
,其中n是一个任取的大于等于1的常数。可以想像,这个函数的分子部分展开后是一个关于x的整系数多项式,最低次数为n,最高次数为2n。我们将用到这个函数的两个性质:首先,当0<x<1时,显然有0 < f(x) < 1/n!;其次,函数f及其任意阶导数在x=0和x=1处都是整数。为了证明后一个结论,首先注意到当x=0时,不管是多少阶的导数,除了常数项以外其余项都是0;常数项只可能在n<=k<=2n时出现(k表示k阶导数),但此时它等于一个整系数乘以k!/n!,显然也是个整数。另外,由于f(x)=f(1-x),根据复合函数的微分法我们立即得到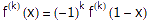 对任意x都成立,当然也就有
对任意x都成立,当然也就有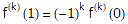 。
。
Read more…
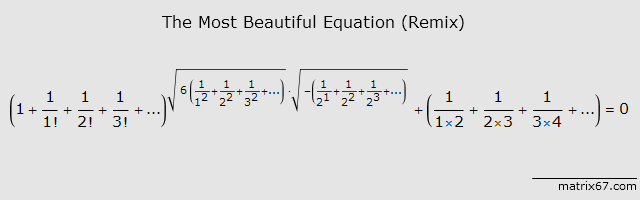

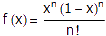 ,其中n是一个任取的大于等于1的常数。可以想像,这个函数的分子部分展开后是一个关于x的整系数多项式,最低次数为n,最高次数为2n。我们将用到这个函数的两个性质:首先,当0<x<1时,显然有0 < f(x) < 1/n!;其次,函数f及其任意阶导数在x=0和x=1处都是整数。为了证明后一个结论,首先注意到当x=0时,不管是多少阶的导数,除了常数项以外其余项都是0;常数项只可能在n<=k<=2n时出现(k表示k阶导数),但此时它等于一个整系数乘以k!/n!,显然也是个整数。另外,由于f(x)=f(1-x),根据复合函数的微分法我们立即得到
,其中n是一个任取的大于等于1的常数。可以想像,这个函数的分子部分展开后是一个关于x的整系数多项式,最低次数为n,最高次数为2n。我们将用到这个函数的两个性质:首先,当0<x<1时,显然有0 < f(x) < 1/n!;其次,函数f及其任意阶导数在x=0和x=1处都是整数。为了证明后一个结论,首先注意到当x=0时,不管是多少阶的导数,除了常数项以外其余项都是0;常数项只可能在n<=k<=2n时出现(k表示k阶导数),但此时它等于一个整系数乘以k!/n!,显然也是个整数。另外,由于f(x)=f(1-x),根据复合函数的微分法我们立即得到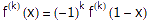 对任意x都成立,当然也就有
对任意x都成立,当然也就有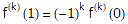 。
。