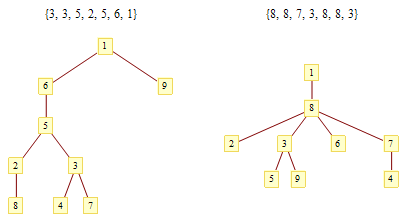
Cayley公式是说，一个完全图K_n有n^(n-2)棵生成树，换句话说n个节点的带标号的无根树有n^(n-2)个。今天我学到了Cayley公式的一个非常简单的证明，证明依赖于Prüfer编码，它是对带标号无根树的一种编码方式。
给定一棵带标号的无根树，找出编号最小的叶子节点，写下与它相邻的节点的编号，然后删掉这个叶子节点。反复执行这个操作直到只剩两个节点为止。由于节点数n>2的树总存在叶子节点，因此一棵n个节点的无根树唯一地对应了一个长度为n-2的数列，数列中的每个数都在1到n的范围内。下面我们只需要说明，任何一个长为n-2、取值范围在1到n之间的数列都唯一地对应了一棵n个节点的无根树，这样我们的带标号无根树就和Prüfer编码之间形成一一对应的关系，Cayley公式便不证自明了。
Read more…
图论
一个与矩形剖分有关的命题（二）：直观的图论证明
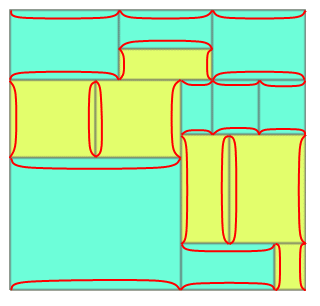
接下来，我们用图论方法来证明：一个由小矩形拼接而成的大矩形，若每个小矩形都有至少一条整数长的边，则大矩形也有至少一条整数长的边。考虑图中每个矩形的每个顶点，把它们作为图G的顶点集（相邻矩形重合的顶点并作一个点）；对于每一个小矩形，把它整数边方向的两对顶点分别用一条边连接起来（相邻矩形公共边上的重边不合并）。如果哪个小矩形四条边都是整数，无妨随意把它当作横向整数边的或者纵向整数边的，连接任一种方向上的边。这样的话，每个矩形恰好产生两条边。注意这个图的一些很显然的性质：度为1的点只有4个（大矩形的四个角），其余的顶点的度都是偶数（只能是2或者4）。下面，我们把这个矩形放在平面坐标系上，大矩形的左下角对齐原点(0,0)。从原点开始沿着图G的边走（每条边最多走一次，不走走过的边），显然走到的每个点都满足这个性质：它的两个坐标均为整数。但我们的出发点是一个度为1的点，在走到另一个度为1的点之前，我们遇到的所有顶点的度都是偶数。因此只要没走到另一个度为1的点，我们就不可能走死。但是，图G总的边数有限，总有一个时候我们将不能再走。因此，这次旅程的终点必然落在另一个度为1的点上。这个终点是大矩形的另一个角，它的两个坐标值均为整数。命题得证。
Ubigraph：强大而易用的图论动画生成软件
Ubigraph是一个全新的图论动画生成软件，利用它你可以快速生成图论模型的图形和动画，直观地展示出各种图论模型的三维结构，演示各种图论算法的过程，非常适合用于研究和教学。之前本Blog曾经介绍过一个类似的软件graphviz，但这里提到的Ubigraph显然更强大一些。上面的动画就是由Ubigraph生成的二叉查找树演示动画（高清版here），看上去相当的酷。值得一提的是，Ubigraph也是相当易用的。graphviz有它自己的语法规则，而Ubigraph则直接支持Python, Ruby, PHP, Java, C, C++等几乎所有主流语言，因此不管你原先使用的是什么语言，你都可以很快地融入到Ubigraph来。例如，在C语言中包含一个头文件UbigraphAPI.h，你便可以像往常一样用循环语句“画”一个环。
#include <UbigraphAPI.h>
int main(int const argc, const char ** const argv)
{
int i;
for (i=0; i < 10; ++i)
ubigraph_new_vertex_w_id(i);
for (i=0; i < 10; ++i)
ubigraph_new_edge(i, (i+1)%10);
sleep(2);
ubigraph_clear();
}
你可以在这里下载这个软件。目前该软件暂时没有Windows版。
63岁以色列数学家Avraham成功解决公路涂色问题
以色列数学家Avraham Trakhtman最近解决了一个非常有名的数学难题——公路涂色问题(Road Coloring Problem)。这是图论中的一个著名猜想，最早由Benjamin Weiss和Roy Adler在1970年提出。63岁的Avraham用铅笔草草写下了仅仅8页的证明过程，出人意料地解决了这个问题。该问题的解决对道路规划等很多现实社会中的问题都有帮助。
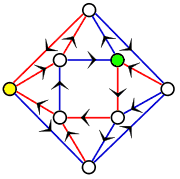
给定一个有向图G（即图中的每一条边都单向地从某个顶点指向另一个顶点），其中每一个点的出度（向外走的边的条数）都为k。假设我们用k种颜色对图G中的所有边进行染色，使得每个点的k条出边的颜色都不相同，并且对于每一个顶点v，总存在一个颜色序列，使得不管你从哪里出发，按照这个颜色序列不断走下去，最终都能到达顶点v。我们称满足这些条件的涂色方案叫做一个同步着色(synchronizing coloring)。Benjamin Weiss和Roy Adler猜想，如果一个有向图是强连通的（任两点间都可互相到达）并且是非周期性的（所有环的长度的最大公约数为1），则该图一定存在同步着色方案。例如，右面这个图就是一个合法的同步着色方案，每个点的两条出边恰好一红一蓝。我们可以找几个点简单验证一下：不管你在哪里，按“蓝-红-红”走最终总会到那个黄色的点；类似地，不断按“蓝-蓝-红”走，不管出发点在哪里你最后总会走到绿色的点。
这个猜想的完整证明过程可以在这篇论文里找到。论文只有几页，估计我应该能看懂，看懂了的话我会更新出来的。
趣题：一个与Hamilton回路有关的问题
今天在回访网站流量来源时看到了一个很牛B的东西，和大家分享一下。
给定一个顶点数为100000的图G，问是否存在Hamilton回路。现在，A宣称自己已经找到了一个Hamilton回路，但B不信，要A证明给他看。你能否想出一个办法使得，A可以让B相信自己有了正确的答案，但B依然不知道答案是什么。这种方法既科学又有趣，整个过程不需要第三者参与，仅仅靠AB两人之间的交流即可。这种方法可以让B有充分的理由相信A找到了Hamilton回路，但能保证B仍然得不到任何与正确答案有关的线索。
首先，A生成一个100000的全排列P，然后用这个排列P把原图G的顶点标号打乱（对标号进行置换），这样就得到了一个同构的图G'。然后A把图G'告诉给B。注意，目前判断两个图是否同构还没有有效的P算法，因此除非A把排列P也告诉了B，否则B不知道G'和G是不是真的同构。接下来B从下面这两个问题中随机抽一个问题让A作答：叫A证明G与G'同构（即叫A给出排列P，确保他没有作假），或者叫A指出G'中的一条Hamilton回路。反复进行“构造G'—抽问”的过程，每次A答对后B都会更加确信A确实找到了原图G的Hamilton回路，来个十几二十次后A作假的嫌疑基本上可以被排除了。这是因为，如果A不知道原图G中的Hamilton回路，这两个问题他是不可能同时答对的，既然B是抽查的，A不可能每次总能答对。同时，除非B同时知道了两个问题的答案，否则B永远不知道原图G的Hamilton回路是什么。仅仅知道G'的Hamilton回路是没有用的，因为此时B连G和G'是否同构都不知道，更别提找出它们之间的对应关系了。
来源：http://www.zju88.cn/cgi-bin/bbstcon?board=Algorithm&file=M.1200769543