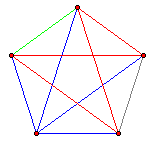
一个完全图K_n是指一个有n个顶点的图，其中每两个点之间都有一条边相连。一个完全二分图是指这样一种图，图中的顶点分为两个点集L和R，L里的每个顶点都和R里的所有点相连。上图显示了一种把K_5划分为四个完全二分图的方法（分别用红蓝绿灰四种颜色来表示这四个子图）。你觉得，最少可以把完全图K_n划分成多少个完全二分图？给出一种划分方案，并证明这个数目已经不能再少了。
图论
经典证明：环面上的七色定理
有时候，一个看似更加复杂的问题反而有一个更简单的解答。
四色问题是说，对一个平面地图进行染色，要想用不同的颜色来区别相邻的区域，最少需要多少种颜色。在很长一段时间里，人们猜想，只要四种颜色就足够了；但这个“四色猜想”却怎么也证不出来。直到上世纪70年代，“四色猜想”才在计算机的帮助下获得证明。在《从一到无穷大》一书中，作者提到了这样一个有趣的事实：平面上的四色问题一直是一个相当复杂的难题，然而有意思的是，在环面上的染色问题却只需要短短十几行文字就能得出一个完美的结论。下面我们来说明，给一个游泳圈上任意划分出来的区域进行染色，为了使相邻区域不同色，只需要7种颜色就够了。
为了证明这一点，我们只需要说明，在一个环面图中总能找到一块区域，它的邻域不超过6块。如果真是这样的话，余下的部分用数学归纳法就直接证到了：对于一个有n个区域的图，我们找出它的一个邻域数量不超过6的区域，然后把这块区域缩小为一个点，使整个图的区域个数减少到n-1。按照我们的数学归纳，这个有n-1个区域的图是可以7染色的；并且显然地，把第n个区域添加回去后所产生的图仍然可以7染色，因为我的邻域不超过6个，我总能找一个和这些邻域都不一样的颜色。
现在的问题就是，为什么总存在邻域数量不超过6的区域呢？注意到在环面上，有V+F-E=0，其中V表示顶点数，F表示区域数，E表示边的总条数。注意到每个顶点都发射出了至少三条边，即所有顶点引出的边数至少为3V；但每条边都被重复计算了一次（因为一条边有两个端点），因此3V/2≤E，即3V≤2E。代入V+F-E=0，得到E≤3F。假设每个区域都有7个或7个以上的邻域，那么它们将产生至少7F条边；但每条边都被重复计算了一次（因为每条边都为两块区域共享），因此7F/2≤E，即7F≤2E。于是，2E≥7F>6F≥2E，矛盾。
趣题：奇怪的有向图 任两点间两步之内可达的路径有且仅有一条
有这么一个无自环的有向图，它的顶点数在30和40之间（包括30和40）。对于图里面的任意两个点A和B，要么存在一条有向边A->B，要么存在唯一的一个“中间点”C使得A可以通过A->C->B两步走到B。换句话说，对任意给定的A、B两点，从A到B的长度不超过2的路径有且仅有一条。注意，即使当A=B时，这个条件也是成立的。试问这个图有多少个顶点。
趣题：2n+1个点中任n个都与同一点相连，则存在一个连接所有点的点
有2n+1个人，他们的朋友关系满足这样一种奇特的性质：任选n个人，则在剩下的人中总能找到一个人，他和这n个人都是朋友。求证，存在这样一个人，他和所有人都是朋友。我们假设朋友关系是双向的，也就是说如果A是B的朋友，那么B一定是A的朋友。
这明显可以转化为一个图论问题。选出两个互为朋友的人。我们得到了一个大小为2的团（一个“团”就是一个所有结点两两相连的子图，或者干脆说是完全图形状的子图）。和另外n-2个人并在一起，则存在一个人和他们都是朋友（当然和那两个人也就是朋友了）。把这个人加进刚才那个团里，于是我们得到了一个大小为3的团。又随便取n-3个人和这3个并在一起，则有一个人和所有这些人都是朋友，于是我们继续扩展出一个大小为4的团。反复进行这个操作，直到我们得到一个大小为n+1的团，此时团的大小已经不能再继续扩展了。但是，一旦注意到此时不属于团的人只剩n个了时，我们发现问题已经解决了：在团里面存在一个人P，他和不属于这个团的那n个人都是朋友。而P本身在一个大小为n+1的团里面，他和团里的其余n个人都是朋友。因此，P和所有人都是朋友。
来源：http://www.cut-the-knot.org/arithmetic/combinatorics/Clique.shtml
趣题：循环赛中总存在一人“可传递一次”地打败了所有人
n个人中每两个人之间都进行过一次比赛。假设比赛不可能出现平局。证明，一定能找出这样的一个人，对于其它任何一人p，他击败了p或者击败了某个打败了p的人。
一句话证明：赢的次数最多的那个人显然满足我们的条件。反证，假设被他打败的所有人的集合为P，万一有个人既没有输给他，也没有输给P里面的任何一人，那这个人至少赢了|P|+1次，成了获胜次数更多的人，矛盾。我故意在这里多写一句话，目的是想说明前面的空白有多短。在Ctrl+A之前，不妨试试看自己能否想到如此简单的证明。
来源：http://www.cut-the-knot.org/arithmetic/combinatorics/RoundRobinTournament.shtml