07年5月12日晚我举办了一次OI生日邀请赛,比赛已经顺利结束。下面是这次比赛的全部试题:
题目一览
题目名称 为什么最少 身高控制计划 狼的复仇 和MM逛花园
题目类型 传统 传统 传统 传统
源文件名称 whyleast.(pas/c/cpp) height.(pas/c/cpp) wolf.(pas/c/cpp) garden.(pas/c/cpp)
输入文件名 whyleast.in height.in wolf.in garden.in
输出文件名 whyleast.out height.out wolf.out garden.out
时间限制 1秒 1秒 1秒 0.1秒
内存限制 64M 64M 64M 64M
测试点 10个 10个 10个 10个
分值 100分 100分 100分 100分
Problem 1: whyleast
为什么最少
问题描述
时间过得真快,16号就是我的19岁生日了。为了让自己在新的一岁里人品加加,本菜鸟特地准备了原创菜题大餐供各位大牛享乐,希望大家人人400分。我们今天的第一题巨菜无比,此题乃经典的Hanoi塔问题。在1号塔上有n个盘子,你需要按照Hanoi塔的要求把所有的盘子都移动到3号塔上。
我一直想不通的是,为什么那些智力题总是要求人们用最少的步骤完成题目中的要求。为什么非要最少呢?这次我们来点特别的,我希望你的程序能够用最多的步数达到要求,而且在此过程中不重复出现任何一种状态。
输入数据
输入数据只有一个正整数n,表示Hanoi塔问题的金片个数。
输出数据
第一行输出在不重复出现状态的情况下完成n阶Hanoi塔的最多步数。
以下若干行依次表示你的操作步骤,每一行两个数a,b表示在这一步应该把a号柱最顶上的金片移动到b号柱上。
如果有多种方案,你只需要输出其中一种即可。评测系统可以判断你的方案的正确性。
样例输入
2
样例输出
8
1 2
2 3
1 2
3 2
2 1
2 3
1 2
2 3
数据规模
对于所有数据,n<=12。
附:Hanoi塔问题简介(摘自http://www.matrix67.com/blog/article.asp?id=29)
法国数学家艾得渥·卢卡斯(Edouard Lucas)于1883年在一份杂志上介绍了一个引人入胜的数学谜题——汉诺塔(Tower of Hanoi),并称这与古印度的一个传说有关。显然传说的具体内容已经不在本文论述的范围内了,但我想简单的介绍一下。
相传印度有座大寺庙,它曾被认为是宇宙的中心。神庙中放置了一块上面插有三根长木钉的木板,在其中的一根木钉上,由上至下放了64片直径由小至大的圆环形金属片。古印度教的天神指示他的僧侣们将64片金属片全部移至另一根木钉上。移动规则只有两个:
1.在每次的移动中,只能移动一片金属片;
2.过程中任意时刻必须保证金属片小的在上,大的在下。
直到有那么一天,僧侣们能将64片金属片按规则从指定的木钉上全部移至另一根木钉上,那么,世界末日即随之来到,世间的一切终将被毁灭,万物都将至极乐世界。
这个传说经常被认为是卢卡斯教授为推广这个数学谜题而捏造的,但不管怎么说,卢卡斯是成功了。这玩意儿变成了家喻户晓的益智游戏之一,后来又成为了学习递归的必修课程。
Problem 2: height
身高控制计划
问题描述
不要总以为MM只担心自己的体重。经过Matrix67的观察,他发现他身边的MM们更关注自己的身高。MM们都希望自己能长高一些但不要长得太高。如果两个MM的身高相差不多,矮的MM会羡慕较高的MM,希望能长得和她一样修长;如果两个MM的身高相差太大,高的MM反而会想变得和较矮的MM一样娇小。Matrix67为了控制GF们的身高,采取了一项身高控制计划:任意两个女生A和B之间,假设A要比B高一些,如果A高出B的1/4,则A应该以B的身高为目标;相反,如果A的身高小于等于B的1.25倍(但仍然比B高),则B应该努力向A的身高看齐。我们假设不存在身高相等的MM。这样,Matrix67的n个MM之间产生了n(n-1)/2个单向的“榜样”关系。
之后,Matrix67发现,这样的关系设定存在一个问题:有可能出现A以B为学习目标,B以C为学习目标,C又以A为学习目标的情况。这不相当于自己是自己的榜样么?这样的循环非常可笑,显然是不科学的。Matrix67希望调整一些关系的方向从而消除所有的循环。Matrix67每次改变其中一对MM之间的关系方向,你需要写程序判断,每一次改变后n个MM之间的“榜样”关系是否存在循环。
输入数据
第一行输入两个用空格隔开的正整数n和m,分别表示MM的个数和改变方向的总次数。
以下n行每行一个数,其中第i行表示编号为i的MM的身高。为了避免身高相等的情况,高度值已经被“放大”过,所有高度均为不超过2 000 000 000的正整数。
接下来的m行里每行有用空格隔开的两个不相等的正整数A, B,表示Matrix67对编号为A的MM和编号为B的MM之间的单向关系进行反向。
输出数据
&nbs
p; 对于Matrix67的每一次操作,你需要输出是否存在某个MM以自己为学习目标的情况(即关系图中是否存在循环)。如果是,则输出“YES”,如果不是,请输出“NO”。
你的输出应该有m行。
样例输入
4 3
10
7
8
9
3 4
1 2
4 1
样例输出
YES
NO
YES
样例说明
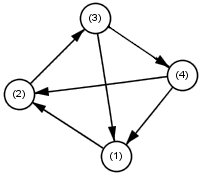
10超过了7的5/4,因此身高为10的MM向身高为7的MM学习;
10小于等于8的5/4,因此身高为8的MM向身高为10的MM学习。
同样地,还有9–>10,7–>8,9–>7,8–>9。
这一组关系中存在多个循环,比如①–>②–>③–>①,再比如①–>②–>③–>④–>①。
第一次Matrix67将改变③和④之间的方向,这消除了上述第二个循环,但前一个循环仍然存在。
第二次Matrix67将改变①和②之间的方向,此时关系图中已经不存在循环了。
第三次Matrix67改变了①和④之间的方向,这将导致新的循环①–>④–>③–>①的出现。
数据规模:
对于30%的数据,n<=10, m<=100;
对于50%的数据,n<=100, m<=1000;
对于70%的数据,n<=1000, m<=100 000;
对于100%的数据,n<=100 000, m<=100 000。
Problem 3: wolf
狼的复仇
问题描述
山谷里有n座森林,这些森林从1到n编号。某些森林之间有小路相连,总共m条小路连通了这n座森林,任意两座森林之间都有至少一条路径可以互相到达。
很久很久以前,这里是狼的家园。在每一座森林里都有一匹狼,每一匹狼都静静地守护着它所在的森林。直到有一天,人类出现了。它们疯狂地开垦1号森林,并且杀死了1号森林的狼。以后,这座森林就好像属于人类了一样,不时有人来到1号森林。其余的n-1匹狼不愿看到悲剧再次发生,它们希望集合它们的力量,为种族,为大自然报仇。
机会来了。一次偶然的机会,大灰狼们获得了一个重要的情报——有一个小MM经常独自游荡于1号森林。消息传遍了整个狼群,小MM细腻的皮肤和鲜嫩的肉令它们的血液沸腾起来,每一匹狼都幻想着能扑上前去撕裂MM的身体,舔拭那温热的血液。唯一的问题是,它们需要尽快察觉小MM的出现并快速奔向目的地。但由于山谷地形复杂,在第一时间里观察到小MM的出现谈何容易。因此,狼群计划在某些森林建立瞭望塔。当小MM再次出现在1号森林里时,所在的森林里有瞭望塔的狼可以立即发现这一情况,并且沿着最短路径奔向MM。有时最短路不止一条,在途中每当有多条路可以选择时,狼总会选择前往编号较小的森林。这些狼的行动将唤起最短路上沿途经过的狼,这些最短路上的狼将会闻声而起,一同对MM发起进攻。每匹狼都有自己的攻击力,最终对小MM的攻击力即是所有到达1号森林的狼的攻击力总和。注意攻击力的值有可能为负数,因为有一些狼很可能会“拖后腿”,对整个种族的复仇计划反而不利。
由于森林的地形不同,在不同的地方建造瞭望塔需要的材料不同。现在狼群里一共有k个单位的建筑材料,并且它们已经计算出在n-1座森林中建造瞭望塔各自需要的材料数目。请你来计算一下,在哪些森林里建造瞭望塔可以使得最终到达1号森林的狼群攻击力总和最大。当然,建筑材料不一定要全部用完,但你的方案所需要的建筑材料不能超过总的材料数k。
输入数据
第一行输入三个用空格隔开的正整数k, n, m,分别表示材料的总数量,森林的数量和小路的数量。1号森林总是MM出没的地方,其余n-1座森林是狼所在的地方。
第二行到第n行每行有两个用空格隔开的整数,依次表示2号森林到n号森林里的狼的攻击力和在这里建造瞭望塔所需要的材料数。狼的攻击力绝对值不超过10000(可能为负数),每个瞭望塔的材料耗费都是不超过100的正整数。
接下来m行每行有三个用空格隔开的数x,y,d,表示在x森林和y森林之间存在一条长度为d的路。路的长度是不超过10000的正整数。
输出数据
输出在满足材料数限制下建造瞭望塔,最多可以给MM带去多大的攻击力。
样例输入
8 7 10
1 4
1 2
2 4
-3 5
9 4
2 1
1 4 2
4 3 4
2 3 3
5 1 2
2 4 1
1 2 3
6 7 1
2 7 4
2 6 8
5 6 5
样例输出
10
样例说明
输入数据如下图所示,我们用AP来表示攻击力,用cost来表示瞭望塔的材料花费。在涂有蓝色的节点上建造瞭望塔花费仅为7,由于7<=8,因此这种方案未超过材料预算。我们下面计算这种方案所带来的攻击力。
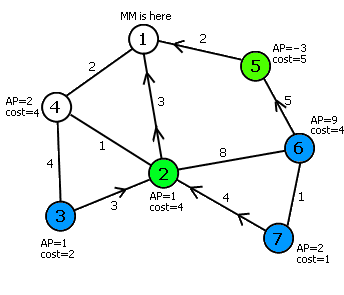
这三匹狼的行走路线已经用箭头表示了出来。注意3号森林和7号森林的狼有多个到达节点1的最短路径,它总是选择标号较小的节点前进。这些路线经过了两个绿色的节点,这两个绿色的节点所对应的狼的攻击力也将加入总攻击力中(必须加入计算且仅算一次)。这种方案的攻击力为1+1+2+9-3=10。事实上,攻击力最大为10,没有其它的建造方案使得总攻击力大于10且材料花费不超过8。
数据规模
对于30%的数据, k<=1, n<=10, m<=100
对于50%的数据, k<=10, n<=100, m<=1000
对于100%的数据,k<=100, n<=1000, m<=10000
Matrix67提醒各位女同学:独自外出时请注意安全。
Problem 4: garden
和MM逛花园
问题描述
花园设计强调,简单就是美。Matrix67常去的花园有着非常简单的布局:花园的所有景点的位置都是“对齐”了的,这些景点可以看作是平面坐标上的格点。相邻的景点之间有小路相连,这些小路全部平行于坐标轴。景点和小路组成了一个“不完整的网格”。
一个典型的花园布局如左图所示。花园布局在6行4列的网格上,花园的16个景点的位置用红色标注在了图中。黑色线条表示景点间的小路,其余灰色部分实际并不存在。
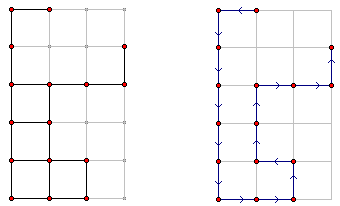
Matrix67的生日那天,他要带着他的MM在花园里游玩。Matrix67不会带MM两次经过同一个景点,因此每个景点最多被游览一次。他和他的MM边走边聊,他们是如此的投入以致于他们从不会“主动地拐弯”。也就是说,除非前方已没有景点或是前方的景点已经访问过,否则他们会一直往前走下去。当前方景点不存在或已游览过时,Matrix67会带MM另选一个方向继续前进。由于景点个数有限,访问过的景点将越来越多,迟早会出现不能再走的情况(即四个方向上的相