
– 我讨厌“快速增长5厘米”之类的垃圾邮件
– 操!我他妈的连向量都还不是呢!
来源:http://brownsharpie.courtneygibbons.org/?p=508
另,可爱的叉烧妖MM给我推荐了一个有意思的东西,大家可以去看看。

官方网站:http://www.math.cmu.edu/~fho/jenn/
Windows版下载:http://www.math.cmu.edu/~fho/jenn/jenn3d_win_2008_01_15.zip
想知道各种几何模型在超球面(四维球的球面)上的样子吗?这个程序可以把各种几何体映射到超球面上,然后用三维的方式展示出来。你会发现几何体的棱和面都是弯的,这是因为这些几何体是在四维球面中的。就像三维球表面上的赤道和两根经线组成的“三角形”一样,每条边都是弯的。
当然,最神奇的还是在这样的空间里下围棋!
Windows版超球面围棋程序下载:http://www.math.cmu.edu/~fho/jenn/jenngo_win.zip
双击左键下黑子,双击右键下白子;左键拖动旋转,右键拖动遍历第四维。
你会发现,这个空间在边界处与自身相交。
今年一月份,California的一个数学艺术展览会上出现了这样一种神奇的三维图形。放出图片之前,你能根据下面的文字描述想象出这个图形的样子吗?
给定一个单位大小的立方体,在其中5个面的中心放置一个边长为1/2的小立方体;这5个小立方体中的每一个都有5个面露在外面,在这25个面中的每一个面中心再向外拼接一个边长为1/4的小立方体;然后每个1/4小立方体的5个暴露在外的面上再放置1/8大小的立方体……不断迭代下去后,最终会形成一个什么样的三维图形?

上图就是按照要求迭代11次的样子,里面那个斜着放的红色立方体是最初的那个单位立方体,外面拼接了5个橙色立方体,每个橙色立方体外面又拼接了5个黄绿黄绿的小立方体……最终的形状大致是一个四棱锥,上面有很多三角形的洞,这些被挖去的部分恰好组成了最经典的分形图形——Sierpinski三角形。这是由艺术家Robert Fathauer发现的,在展览上的名字叫做Fractal Crystal No.1。
查看更多:http://www.bridgesmathart.org/art-exhibits/jmm08/

来源:http://digg.com/pc_games/Portal_MC_Escher_Style
Portal是我所玩过的最棒的游戏!!
Update: 图片的原型是错觉大师M.C. Escher的版画。你在网上看到的错觉图片有一半都是他的(比如那个不可能瀑布建筑、走不完的楼梯、两只互相绘制的手、Möbius带上的蚂蚁)。这幅名为Relativity的版画是M.C. Escher的代表作之一。
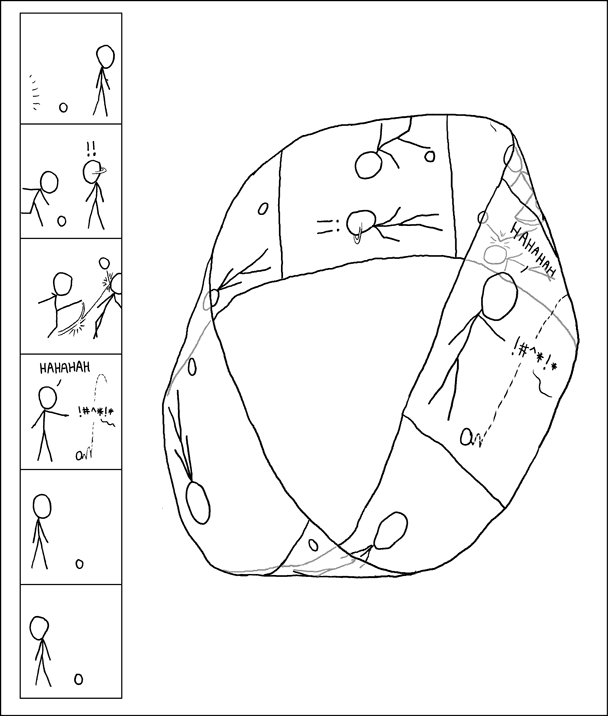
图片来源:http://xkcd.com/381/
知道最妙的是什么吗?是那句HAHAHAH。因为字母H和A恰好都是左右对称的,而且后面多加了一个H使得这句话也变成了回文串。此外,那句!#^*!*也不是随便乱写的。