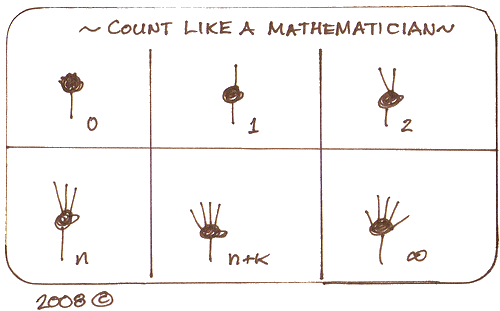大家都知道,三角形具有稳定性。如果你把三根木条钉成一个三角形,则这几根木条是不能活动的。这是因为,根据三角形的SSS全等判定法则,两个三角形的三边长对应相等,则这两个三角形一定全等。但四边形就不是了,用四根一样长的木条钉成一个正方形,握着相对的两个角往两边一拉,正方形就变成菱形了。不知道大家想过没有,类比到三维空间中,多面体的稳定性又是怎样的呢?
Cauchy定理指出,如果两个凸多面体对应的面全等,那么这两个多面体全等。这告诉我们,任何一个凸多面体一定都是不可活动的。在Cauchy定理中,“凸多面体”这一条件是必需的。如果允许凹的多面体存在,对应面相等但整个多面体不全等的形状可以很轻易地构造出来。例如,想象立方体的某个面中心有一个小金字塔,这个金字塔既可以是向外凸的(就像表面上的一根刺),也可以是向内凹的(表面上的一个坑);这是两个截然不同的多面体,但它们的对应面都是相等的。不过,这与我们的稳定性并没有关系,因为它并不是做连续的变形,而是直接一下就“跳”过来了。
很长一段时间,人们曾经猜想,不存在可以做出连续变形且保持所有面不变的“可活动多面体”(Flexible Polyhedron)。1978年,Connelly找到了第一个反例。他给出了一个由18个面组成的可活动多面体。
图片
Typography Art: Mathematical Induction

挖到一张好图,做成海报贴在墙上会很酷。
来源:http://fiveless.deviantart.com/art/mathematical-induction-56305755
我很喜欢Typography Art。最喜欢这个。
Count Like a Mathematician
Oh 一层一层 一层一层 一层一层 又一层层的Klein瓶
立体图与三维数据展示
 我的左眼有相当严重的散光,因此无缘各种类型的3D立体图,包括看对眼、立体眼镜、左右两幅图(一只眼睛看一个)等等。后来,网上出现了一种只需要一只眼睛就能体验的3D图,原理非常简单,效果也比较震撼。只需要在两个眼睛的位置分别拍照,然后做成gif循环显示两个图片,大脑也可以从中迅速获取信息分辨出第三维来。闲逛ffffound时偶然发现这个图,突然想到:同样的方法为何不用于展示三维数据呢?于是试着用Mathematica做了一个。Mathematica输出gif动画相当简单,只需要一句Export[“file.gif”,{g1, g2, …}]就行了。在这里,我们将用三维空间的点来展示组合数的各位数字之和的分布情况。可以看到,使用3D动画的效果非常明显。
我的左眼有相当严重的散光,因此无缘各种类型的3D立体图,包括看对眼、立体眼镜、左右两幅图(一只眼睛看一个)等等。后来,网上出现了一种只需要一只眼睛就能体验的3D图,原理非常简单,效果也比较震撼。只需要在两个眼睛的位置分别拍照,然后做成gif循环显示两个图片,大脑也可以从中迅速获取信息分辨出第三维来。闲逛ffffound时偶然发现这个图,突然想到:同样的方法为何不用于展示三维数据呢?于是试着用Mathematica做了一个。Mathematica输出gif动画相当简单,只需要一句Export[“file.gif”,{g1, g2, …}]就行了。在这里,我们将用三维空间的点来展示组合数的各位数字之和的分布情况。可以看到,使用3D动画的效果非常明显。
img = ListPointPlot3D[
Table[Total[IntegerDigits[Binomial[i, j]]], {i, 0, 50}, {j, 0, 50}],
ViewVertical -> {0, 0, 1}, ImageSize -> 600];
Export["F:\file.gif", {Show[img, ViewVector -> {-32, -20, 60}],
Show[img, ViewVector -> {-31, -21, 60}]}];
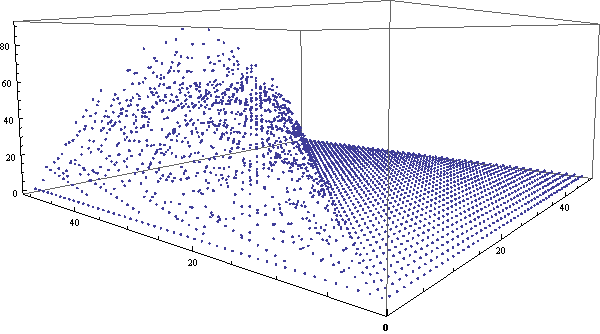
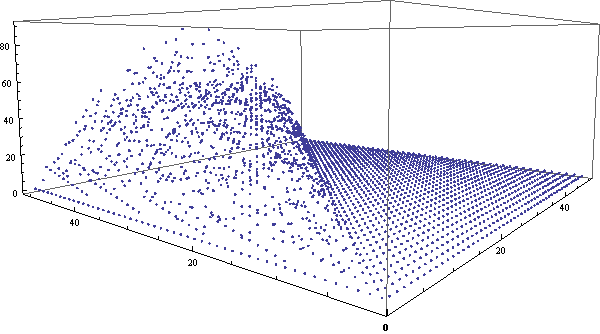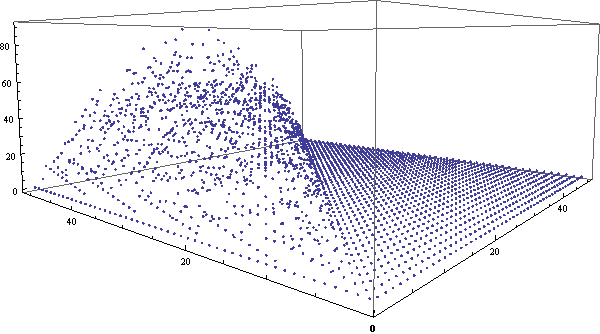
类似地,我们还可以做出环视一周的gif动画来,虽然这样将很难观察出细节,但对总体的把握效果将更好。