四维

令人敬畏的十维空间

/ 50 条评论


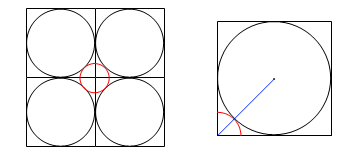
    我们把一个边长为2的正方形划分成4个小正方形，每个小正方形里作一个内切圆，然后在原来的大正方形中间作一个同时外切于这4个圆的小圆（红色标注）。我们把这个小圆叫做“中心圆”。你怎么来求这个中心圆的半径？
    仔细观察其中一个小正方形，思路就出来了：红色的中心圆变成了一个90度扇形，它的中心位于单位正方形的一角，并且外切于直径为1的圆。可以看到扇形半径加上圆的半径等于单位正方形对角线的一半，这样我们就得出，中心圆的半径等于(sqrt(2)-1)/2。
    对于一个立方体同样如此。我们把立方体切成8个小立方体，得到的8个球体中间夹住的那个中心球半径就应该为(sqrt(3)-1)/2。你会发现一个惊人的事实，在超立方体中，位于16个四维球体间的中心球半径为(sqrt(4)-1)/2 = 1/2，它竟然与那16个小球一样大。真正可怕的事情发生在九维立方体中，此时的九维中心球半径为(sqrt(9)-1)/2 = 1，竟然内切于最初的九维立方体！而到了十维空间后，中心球的直径将超过十维立方体的边长，这个中心球将突破立方体的边界！被围在里面的中心球居然比原来的N维立方体还大，这显然违反了大多数人的直觉；如果你能想象出这个画面来，你就牛B了。科幻小说中把对十维空间的感知能力作为文明发达程度的标准，除了一些相关的宇宙模型外，这可能也是其中一个原因吧。

切实感受四维空间

/ 9 条评论

    我跟一些人描述过四维空间。但一个由八个全等立方体拼接组成的广义空间确实让活在三维世界的人难以想像。正如生活在二维空间里的人无法想像在一个扁平的面里怎么可能存在六个全等正方形互相拼接组成的立体形状。我们通常只能在一张纸上画四条射线并令它们两两互相垂直来表现四维空间。但第四维究竟在哪里？昨天我发现的两个网站可以帮助你感受到。

    如果你对四维立方体还不够了解，下面这个网站叙述了由二维到三维到四维的递推过程，它或许可以帮助你。
http://www.mathematische-basteleien.de/hypercube.htm

    下面两个网站的Java小程序能让人体会到一个四维立方体的存在和它绕第四维旋转的可能。

    首先，你的浏览器必须支持Java。你可以在网上搜索到有关内容。

    下面这个网站是一个通过红-蓝3D立体眼镜图或3D立体图（说穿了，就是用对眼看）能感受到的旋转的四维立方体。
http://dogfeathers.com/java/hyprcube.html
    从三维的角度而不是一张薄纸能快速感到四维立方体如何绕第四维旋转。找一个眼镜，把左边的镜片涂成红色，右边蓝色，使得你左右眼分别看到两种不同颜色的线条。戴上后你将能看到真实的立体感。在花店分别找一张红色和蓝色的玻璃纸也能轻易地做到这一点。另外，点击stereo两次后，可以用看3D立体图的方式 “对眼”去看，但效果没有那么好。

    下面这个网站提供了一种4D环境中的游戏。
http://www1.tip.nl/~t515027/hypercube.html
    在这个游戏中，你需要在三维或四维立方体中把球撞击到标记的位置，然后从出口出去再进来以获得另外一个标记，并尽量不要被外面的小球看到。成功撞击5次标记后游戏结束，你可以看看自己的得分。游戏分为两种：三维的和四维的。每一种游戏都可以选择是否启用立体图模式（看对眼模式）。比如，在三维的游戏中，不开启立体图模式你很难判断前后的位置关系，需要自己的空间想像能力。而开启立体图模式后，你将能清晰地看到三维空间中各物体的位置关系。你可以先试着在三维立方体中关掉立体模式玩这个游戏，就像是玩一个2D游戏一样。然后在四维立方体中开启立体模式玩，就像是玩一个3D游戏一样。过一会儿，你将会发现你能自由的在四维立方体中移动。

    做人要厚道，转帖请注明出处。