原创Geek图一枚
四维
不同维度的对话：带你进入四维世界
上次说到维度时，有人提到了如何理解四维空间的问题。这是一个非常有趣的话题，可是我一直没有用心写一下。前段时间网上出了一部片子叫做Dimensions: a walk through mathematics，据称里面详细介绍了四维空间。我本以为推荐一下这个片子就能少写一篇又臭又长的日志了的，没想到下下来看了之后发现该片奇差，不了解四维空间的人看了半天估计还是不了解四维空间。最近放假比较闲，打算慢慢来扯一下。如果你以前从来没细想过四维空间的话，相信今天你会有一种超凡脱俗的感觉。
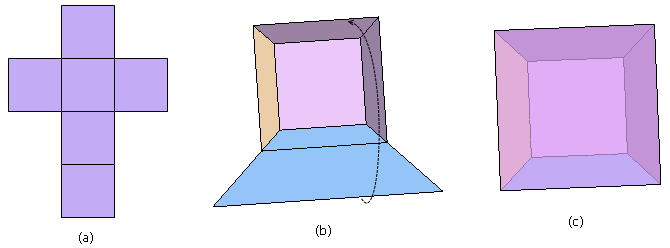
现在，假设我是一个二维世界的人，我不能理解什么是“高度”，什么是“体”，什么是“空间”。你想向我描述三维世界中的立方体。你该怎么说呢？你或许会从立方体的展开图开始谈起：图(a)就是一个立方体的展开图，如果我们剪一个这种形状的纸板，我们可以把它折成一个正方体。我开始好奇了。
假如人类生活在1000维空间里……
偶然看到这个网页，很是受启发，然后自己也没事干，一个人躺在床上想了很多。
昂贵而奢侈的房间
制造一个房间将变得非常的昂贵，也将变得非常非常奢侈。为了建造一个1000维的立方体空间，你需要在2000个方向上各修建一个999维的墙，即使墙的“厚度”很小很小，这也需要耗费大量的人力、物力和财力。同时，这样的房间也将非常非常非常大。假设1000维空间中的人是一个边长一米的超立方体，边长两米的超立方体房间里可以容纳10^300个人。当然，也许有人会问，为什么不把房间边长定小一些呢？如果房间边长仅有1.01米，容量也超过20000了啊？其实，房间容量大了没有任何意义，人多了照样挤不下。正如把一个单位大小的三维立方体放进边长为1.5米的三维立方体盒子中一样，虽然余下的空间超过了两立方米，但这点空间仍然不可能挤下哪怕再多一个的单位立方体。
死一般的世界
不要对高维世界抱有任何美好的幻想。1000维世界里是一片黑暗的。在1000维世界中，发光体再也牛B不起来了。半径为2的超球体，体积是单位超球体的10^300倍；因此随着与光源的距离的增加，照度以难以想象的恐怖速度垂直递减。类似地，1000维世界也是无声的。要想让声音传到10米外的地方，需要耗费的能量是一个天文数字。
在这样的世界中，生物将无法进行远程交流，甚至不会进化出视觉和听觉能力。一切社交行为都是以直接接触的形式发生的。另外一种可能是，当被动接收外界能量不可能实现时，生物将进化出一种主动探测外部世界的能力。生物可以发出一种集中程度高、不易向四周弥散的能量束，该能量束能够沿原路返回，使得生物能定向地获取外部信息。
正如宇宙射线、暗物质、反物质等一些我们（或许是因为缺少某种感觉器官而）感受不到，但事实上确实存在的东西一样，1000维世界中的科学家猜想有光源、声源等自然能量产生。他们投入了大量精力，耗尽了身边可用的资源，企图创造出一个可测量的尺度下的能量源。发现自然的光源和声源将成为物理学界的前沿科学，或者被宗教利用，成为一种具有蛊惑性的仪式。
视频推荐：Dimensions – A walk through mathematics
刚在sdyy那儿看到了这个好东西。影片Dimensions长约2个小时，共分为9章，谈论了维度、射影、复数等有趣的数学话题。下面是一个4分钟长的预告片。完整的视频可以在这里下载。
趣味小程序Jenn3D：带你进入神奇的超球面空间
官方网站：http://www.math.cmu.edu/~fho/jenn/
Windows版下载：http://www.math.cmu.edu/~fho/jenn/jenn3d_win_2008_01_15.zip
想知道各种几何模型在超球面（四维球的球面）上的样子吗？这个程序可以把各种几何体映射到超球面上，然后用三维的方式展示出来。你会发现几何体的棱和面都是弯的，这是因为这些几何体是在四维球面中的。就像三维球表面上的赤道和两根经线组成的“三角形”一样，每条边都是弯的。
当然，最神奇的还是在这样的空间里下围棋！
Windows版超球面围棋程序下载：http://www.math.cmu.edu/~fho/jenn/jenngo_win.zip
双击左键下黑子，双击右键下白子；左键拖动旋转，右键拖动遍历第四维。
你会发现，这个空间在边界处与自身相交。