今天是我第一次听说这个故事。

    1933 年，匈牙利数学家 George Szekeres 还只有 22 岁。那时，他常常和朋友们在匈牙利的首都布达佩斯讨论数学。这群人里面还有同样生于匈牙利的数学怪才——Paul Erdős 大神。不过当时，Erdős 只有 20 岁。

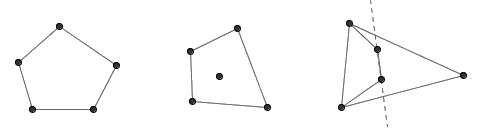
    在一次数学聚会上，一位叫做 Esther Klein 的美女同学提出了这么一个结论：在平面上随便画五个点（其中任意三点不共线），那么一定有四个点，它们构成一个凸四边形。Szekeres 和 Erdős 等人想了好一会儿，没想到该怎么证明。于是，美女同学得意地宣布了她的证明：这五个点的凸包（覆盖整个点集的最小凸多边形）只可能是五边形、四边形和三角形。前两种情况都已经不用再讨论了，而对于第三种情况，把三角形内的两个点连成一条直线，则三角形的三个顶点中一定有两个顶点在这条直线的同一侧，这四个点便构成了一个凸四边形。

Read more…

Johann Carl Friedrich Gauss（1777－1855），史上最牛的数学家。他上知天文，下知地理，涉足数学各个领域，死后都在用未知的神秘力量影响着数学的发展。作为当之无愧的第一大数学家，Gauss 有很多鲜为人知的传奇经历，现在就为你一一八卦：

• Erdős 相信上帝手中有一本包含世间所有精妙证明的天书。上帝相信这本书在 Gauss 手上。
• Gauss 把无穷当作归纳证明中的第一个非平凡的情况。
• Gauss 不用任何公理就能证明一个定理。
• Gauss 不理解什么是 P=NP。在他看来，一切都是常数级别的。
• Gauss 从后往前列举了一下质数，就知道了质数有无穷多。
• Gauss 从来不会用光书本页面边缘的空白。
• Gauss 的 Erdős 数为 -1。
• Gauss 等于自己的幂集。
• Gauss 可以化圆为方，再把它变成一个四维球。
• Gauss 可以既无重复又无遗漏地走遍 Königsberg 的七座桥。
• Gauss 可以用尺规作图三等分角。
• Gauss 可以在六步以内解决骑士周游问题。
• Gauss 同时给 Bertrand Russell 和自己理发。
• Gauss 想喝果汁时，直接对橙子使用夹挤定理。
• Gauss 唱完 “Aleph-Null Bottles of Beer on the Wall” 只用了四分钟。
• Gauss 用 Klein 瓶喝酒。
• Gauss 做俯卧撑时，他不是把自己撑起来，而是把整个地球按下去。
• Hilbert 不能住进 Gauss 旅馆，因为 Gauss 旅馆已经满房了。
• 不是 Gauss 发现了正态分布，而是自然规律遵循着 Gauss 的模型。
• 读了 Gauss 的书之后，Maxwell 决定退出数学界，从事咖啡行业。
• 对于 Gauss 来说，算术公理体系同时满足完备性和一致性。
• 尽管微积分在 Gauss 生前 100 年诞生，但 Gauss 仍然发明了微积分。
• 如果 Gauss 发表了他的所有发现，数学界里就没啥可证的了。
• 有一次，Gauss 和自己玩了一个零和游戏，然后赢了 50 块钱。
• 有一次，Fermat 惹怒了 Gauss，于是就有了 Fermat 最终定理。
• 只有 Gauss 才知道 Schrödinger 的猫是死是活。

来源：http://www.gaussfacts.com （太欢乐了）

    记得第一次了解中文分词算法是在 Google 黑板报 上看到的，当初看到那个算法时我彻底被震撼住了，想不到一个看似不可能完成的任务竟然有如此神奇巧妙的算法。最近在詹卫东老师的《中文信息处理导论》课上再次学到中文分词算法，才知道这并不是中文分词算法研究的全部，前前后后还有很多故事可讲。在没有建立统计语言模型时，人们还在语言学的角度对自动分词进行研究，期间诞生了很多有意思的理论。

    中文分词的主要困难在于分词歧义。“结婚的和尚未结婚的”，应该分成“结婚／的／和／尚未／结婚／的”，还是“结婚／的／和尚／未／结婚／的”？人来判断很容易，要交给计算机来处理就麻烦了。问题的关键就是，“和尚未”里的“和尚”也是一个词，“尚未”也是一个词，从计算机的角度看上去，两者似乎都有可能。对于计算机来说，这样的分词困境就叫做“交集型歧义”。

    有时候，交集型歧义的“歧义链”有可能会更长。“中外科学名著”里，“中外”、“外科”、“科学”、“学名”、“名著”全是词，光从词库的角度来看，随便切几刀下去，得出的切分都是合理的。类似的例子数不胜数，“提高产品质量”、“鞭炮声响彻夜空”、“努力学习语法规则”等句子都有这样的现象。在这些极端例子下，分词算法谁优谁劣可谓是一试便知。

Read more…

    前几天，一篇叫做 用正方形纸片折出等边三角形 的日志引起大家的讨论，折出正七边形和折出角三等分线的方案更是让大家争论不休。提得最多的问题就是，折纸为什么要比尺规作图更强？这是一个好问题。我查了不少资料，了解到不少折纸几何的历史，收获颇大，不赶紧记下来就亏大了。于是有了这篇文章。

    要解答为何折纸如此强大，首先我们得解决一个问题：什么叫折纸。折纸的游戏规则是什么？换句话说，折纸允许哪些基本的操作？大家或许会想到一些折纸几何必须遵守的规则：所有直线都由折痕或者纸张边缘确定，所有点都由直线的交点确定，折痕一律是将纸张折叠压平再展开后得到的，每次折叠都要求对齐某些已有几何元素（不能凭感觉乱折），等等。不过，这些定义都太“空”了，我们需要更加形式化的折纸规则。 1991 年， Humiaki Huzita 指出了折纸过程中的 6 种基本操作（也可以叫做折纸几何的公理）：

   

 1. 已知 A 、 B 两点，可以折出一条经过 A 、 B 的折痕

Read more…

    在准备前一篇日志时，我查阅了很多经典的悖论。我发现，虽说数学悖论大多是一些让人越想越糊涂的逻辑思维游戏，但也有不少悖论来自于实实在在的数学问题。在缺乏现代数学工具的年代，这些反直觉的结论和看似不可调和的矛盾让数学家们百思不得其解，那些最难解决的悖论甚至为数学新分支的开创带来了足够的动机。不太为人熟知的 Cramer 悖论就是一个漂亮的例子。

    在描述 Cramer 悖论之前，让我们先来考虑一个简单的情况。两条直线交于一点。反过来，过一点可以做两条不同的直线。事实上，过一点可以做无数条直线。确定一条直线需要两个点才够。一切都很正常。
    现在，考虑平面上的两条三次曲线。由于将两个二元三次方程联立求解，最多可以得到 9 组不同的解，因此两条三次曲线最多有 9 个交点。另外，三次曲线的一般形式为

      x^3 + a·x^2·y + b·x·y^2 + c·y^3 + d·x^2 + e·x·y + f·y^2 + g·x + h·y + i = 0

    这里面一共有 9 个未知系数。代入曲线上的 9 组不同的 (x, y) ，我们就能得出 9 个方程，解出这 9 个未知系数，恢复出这个三次曲线的原貌。也就是说，平面上的 9 个点唯一地确定了一个三次曲线。这次貌似就出问题了： “两条三次曲线交于 9 个点” 和 “ 9 个点唯一地确定一条三次曲线” 怎么可能同时成立呢？既然这 9 个点是两条三次曲线所共有的，那它们究竟会“唯一地”确定出哪条曲线呢？在没有线性代数的年代，这是一个令人匪夷所思的问题。

Read more…