你或许还记得爱的方程式是什么。
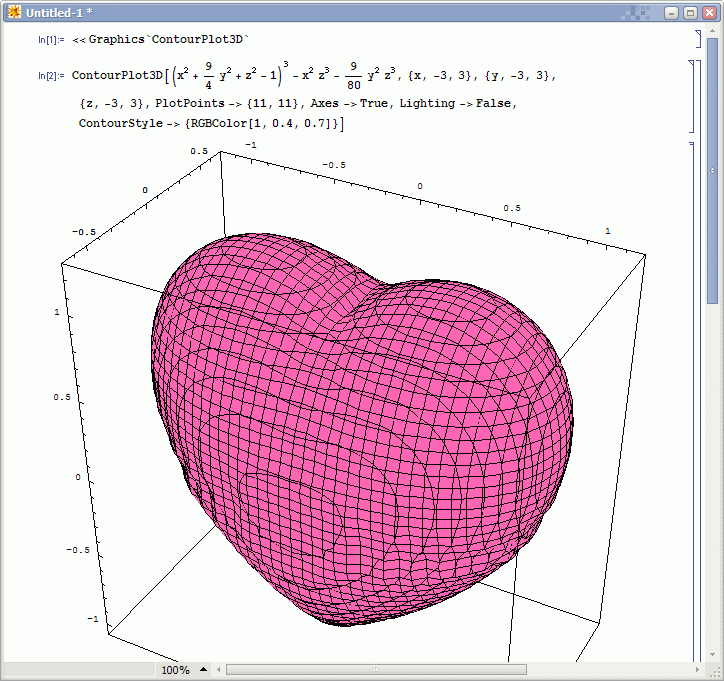
今天我看到了一个加强版,(x^2 + (9/4)y^2 + z^2 – 1)^3 – x^2z^3 – (9/80)y^2z^3 == 0。
下面是本人亲自用Mathematica绘的图,发出来给大家看看。
图片为Matrix67原创
转贴请注明出处
你或许还记得爱的方程式是什么。
今天我看到了一个加强版,(x^2 + (9/4)y^2 + z^2 – 1)^3 – x^2z^3 – (9/80)y^2z^3 == 0。
下面是本人亲自用Mathematica绘的图,发出来给大家看看。
图片为Matrix67原创
转贴请注明出处

康托集合是闭区间[0,1]的子集,它的定义如下:给定区间[0,1],把这个区间分成三段,去掉中间那一端(即去掉(1/3,2/3)),然后把剩下的两段中每一段都按照刚才的方法再进行操作,然后再分,再分,就这样一直挖洞挖下去。在第二次操作后,剩下的区间是[0,1/9]∪[2/9,1/3]∪[2/3,7/9]∪[8/9,1],再操作一次后区间将由8段构成。最后剩下来的东西是什么呢?你能找到存在于这个集合中的某个具体的元素吗(不包括形如x/(3^n)的端点)?
我们看到,n次操作后,区间的总长度为(2/3)^n,当n趋于无穷时,区间长度趋于0。但是这并不能说明这个区间里没有任何元素。事实上,我们可以找到至少一个元素。比如,下图中绿色的点表示三等分点,如果P满足AP/AB=A'P/A'B'的话,那么P点始终以比例相同的位置留在某一段上,这样的话即使无限地分下去也不会把它挖掉。
P点的坐标可以通过解这个方程得到:x/1=(x-2/9)/(1/9)。解出来x为1/4。因此,1/4属于康托集合。当然,除了1/4之外还有很多点在这个集合内,我们只是找到了其中一个。事实上,康托集合内的元素有无穷多个。假如我们把所有0到1的数用三进制表示,那么我们发现,去掉的部分都是三进制小数里有数字“1”的。比如,第一次操作时,1/3和2/3的三进制分别是0.1和0.2,我们去掉的是所有从0.1到0.2的数(不包含端点,因为0.1也可以写成0.0222222222…)。第二次操作就去掉了百分位有1的那些数,依此类推。因此,只要一个位于0和1之间的三进制小数能够只用0和2写出,那么它就属于康托集合,因为它永远不会被去掉。刚才的1/4转化为三进制是0.020202…,因此它属于这个集合。显然,这样的数有无穷多个,比如三进制0.002002002…等于十进制的1/13,因此它也属于康托集合。同样,康托集合里不存在孤点,因为在它的左右可以找出无数个属于康托集合的数。应用对角线方法,这个集合里的元素居然还是不可数的。事实上,我们可以建立康托集合与闭区间[0,1]的一一对应关系。
用以下方法可以把康托集合里的所有数与[0,1]的所有实数对应起来:将康托集合内的任意一个转化为三进制小数后,把每一个数字除以2,再当成是二进制小数转化回来。由于这些三进制小数里只含0和2,因此康托集合里的每个数都恰好能转化为一个[0,1]之间的二进制小数;同样地,二进制小数里的每个“1”变成“2”后也能得到一个康托集合里的数。
设f为定义域在康托集合内的函数,定义f(x)为按照上面的转化方法x所对应的二进制小数,显然这个函数的值域就是[0,1]。比如1/3的三进制为0.0222…,而二进制0.01111…=0.1即十进制的1/2,因此f(1/3)=1/2。我们发现,2/3的三进制为0.2,而0.1的十进制也是1/2。于是f(1/3)=f(2/3)。类似地,那些被挖去的区间的两个端点对应的函数值都相同。现在,我们把这个函数的定义域也扩展到[0,1]:让康托集合里的那些被挖去的区间里的点的函数值与该区间对应的端点相同(在函数图象上看相当于把函数值相等的点用横线段连起来)。于是,f(1/2)=f(1/3)=f(2/3)=1/2,f(1/8)=f(1/9)=f(2/9)=1/4。这个函数一定是上升函数,它在长度为1的区间里从0增长到了1。同时,这个函数也是一个连续函数,因为康托集合与[0,1]的所有实数一一对应。这个函数是一个阶梯状的函数,但是它不是分段的,是连续的。它是无穷多个横线段组成的一个连续函数,除端点无意义以外导数值都是0。或者说,这个函数在不变之中上升。
做人要厚道
转贴请注明出处
我们年级有许多漂亮的MM。一班有7个左右吧,二班大概有4个,三班最多,16个,四班最可怜,一个漂亮的MM都没有,五班据说有1个。如果用一个函数“f(班级)=漂亮MM的个数”,那么我们可以把上述信息表示成:f(1)=7,f(2)=4,f(3)=16,f(4)=0,f(5)=1,等等。
生成函数(也有叫做“母函数”的,但是我觉得母函数不太好听)是说,构造这么一个多项式函数g(x),使得x的n次方系数为f(n)。于是,上面的f函数的生成函数g(x)=7x+4x^2+16x^3+x^5+…。这就是传说中的生成函数了。关键是,这个有什么用呢?一会儿要慢慢说。我敢打赌这绝对会是我写过的最长的一篇文章。
生成函数最绝妙的是,某些生成函数可以化简为一个很简单的函数。也就是说,不一定每个生成函数都是用一长串多项式来表示的。比如,这个函数f(n)=1 (n当然是属于自然数的),它的生成函数就应该是g(x)=1+x+x^2+x^3+x^4+…(每一项都是一,即使n=0时也有x^0系数为1,所以有常数项)。再仔细一看,这就是一个有无穷多项的等比数列求和嘛。如果-1<x<1,那么g(x)就等于1/(1-x)了。在研究生成函数时,我们都假设级数收敛,因为生成函数的x没有实际意义,我们可以任意取值。于是,我们就说,f(n)=1的生成函数是g(x)=1/(1-x)。
我们举一个例子说明,一些具有实际意义的组合问题也可以用像这样简单的一个函数全部表示出来。
考虑这个问题:从二班选n个MM出来有多少种选法。学过简单的排列与组合的同学都知道,答案就是C(4,n)。也就是说。从n=0开始,问题的答案分别是1,4,6,4,1,0,0,0,…(从4个MM中选出4个以上的人来方案数当然为0喽)。那么它的生成函数g(x)就应该是g(x)=1+4x+6x^2+4x^3+x^4。这不就是……二项式展开吗?于是,g(x)=(1+x)^4。
你或许应该知道,(1+x)^k=C(k,0)x^0+C(k,1)x^1+…+C(k,k)x^k;但你或许不知道,即使k为负数和小数的时候,也有类似的结论:(1+x)^k=C(k,0)x^0+C(k,1)x^1+…+C(k,k)x^k+C(k,k+1)x^(k+1)+C(k,k+2)x^(k+2)+…(一直加到无穷;式子看着很别扭,自己写到草稿纸上吧,毕竟这里输入数学式子很麻烦)。其中,广义的组合数C(k,i)就等于k(k-1)(k-2)…(k-i+1)/i!,比如C(4,6)=4*3*2*1*0*(-1)/6!=0,再比如C(-1.4,2)=(-1.4)*(-2.4)/2!=1.68。后面这个就叫做牛顿二项式定理。当k为整数时,所有i>k时的C(k,i)中分子都要“越过”0这一项,因此后面C(k,k+1),C(k,k+2)之类的都为0了,与我们的经典二项式定理结论相同;不同的是,牛顿二项式定理中的指数k可以是任意实数。
我们再举一个例子说明一些更复杂的生成函数。n=x1+x2+x3+…+xk有多少个非负整数解?这道题是学排列与组合的经典例题了。把每组解的每个数都加1,就变成n+k=x1+x2+x3+…+xk的正整数解的个数了。教材上或许会出现这么一个难听的名字叫“隔板法”:把n+k个东西排成一排,在n+k-1个空格中插入k-1个“隔板”。答案我们总是知道的,就是C(n+k-1,k-1)。它就等于C(n+k-1,n)。它关于n的生成函数是g(x)=1/(1-x)^k。这个生成函数是怎么来的呢?其实,它就是(1-x)的-k次方。把(1-x)^(-k)按照刚才的牛顿二项式展开,我们就得到了x^n的系数恰好是C(n+k-1,n),因为C(-k,n)*(-x)^n=[(-1)^n*C(n+k-1,n)]*[(-1)^n*x^n]=C(n+k-1,n)x^n。这里看晕了不要紧,后文有另一种方法可以推导出一模一样的公式。事实上,我们有一个纯组合数学的更简单的解释方法。因为我们刚才的几何级数1+x+x^2+x^3+x^4+…=1/(1-x),那么(1+x+x^2+x^3+x^4+…)^k就等于1/(1-x)^k。仔细想想k个(1+x+x^2+x^3+x^4+…)相乘是什么意思。(1+x+x^2+x^3+x^4+…)^k的展开式中,n次项的系数就是我们的答案,因为它的这个系数是由原式完全展开后k个指数加起来恰好等于n的项合并起来得到的。
现在我们引用《组合数学》上暴经典的一个例题。很多书上都会有这类题。
我们要从苹果、香蕉、橘子和梨中拿一些水果出来,要求苹果只能拿偶数个,香蕉的个数要是5的倍数,橘子最多拿4个,梨要么不拿,要么只能拿一个。问按这样的要求拿n个水果的方案数。
结合刚才的k个(1+x+x^2+x^3+x^4+…)相乘,我们也可以算出这个问题的生成函数。
g(x)=(1+x^2+x^4+…)(1+x^5+x^10+..)(1+x+x^2+x^3+x^4)(1+x)
=[1/(1-x^2)]*[1/(1-x^5)]*[(1-x^5)/(1-x)]*(1+x) (前两个分别是公比为2和5的几何级数,
第三个嘛,(1+x+x^2+x^3+x^4)*(1-x)不就是1-x^5了吗)
=1/(1-x)^2 (约分,把一大半都约掉了)
=(1-x)^(-2)=C(1,0)+C(2,1)x+C(3,2)x^2+C(4,3)x^3… (参见刚才对1/(1-x)^k的展开)
=1+2x+3x^2+4x^3+5x^4+….
于是,拿n个水果有n+1种方法。我们利用生成函数,完全使用代数手段得到了答案!
如果你对1/(1-x)^k的展开还不熟悉,我们这里再介绍一个更加简单和精妙的手段来解释1/(1-x)^2=1+2x+3x^2+4x^3+5x^4+….。
1/(1-x)=1+x+x^2+x^3+x^4+…是前面说过的。我们对这个式子等号两边同时求导数。于是,1/(1-x)^2=1+2x+3x^2+4x^3+5x^4+….。一步就得到了我们所需要的东西!不断地再求导数,我们同样可以得到刚才用复杂的牛顿二项式定理得到的那个结论(自己试试吧)。生成函数还有很多其它的处理手段,比如等式两边同时乘以、除以常数(相当于等式右边每一项乘以、除以常数),等式两边同时乘以、除以一个x(相当于等式右边的系数“移一位”),以及求微分积分等。神奇的生成函数啊。
我们用两种方法得到了这样一个公式:1/(1-x)^n=1+C(n,1)x^1+C(n+1,2)x^2+C(n+2,3)x^3+…+C(n+k-1,k)x^k+…。这个公式非常有用,是把一个生成函数还原为数列的武器。而且还是核武器。
接下来我们要演示如何使用生成函数求出Fibonacci数列的通项公式。
Fibonacci数列是这样一个递推数列:f(n)=f(n-1)+f(n-2)。现在我们需要求出它的生成函数g(x)。g(x)应该是一个这样的函数:
g(x)=x+x^2+2x^3+3x^4+5x^5+8x^6+13x^7+…
等式两边同时乘以x,我们得到:
x*g(x)=x^2+x^3+2x^4+3x^5+5x^6+8x^7+…
就像我们前面说过的一样,这相当于等式右边的所有系数向右移动了一位。
现在我们把前面的式子和后面的式子相加,我们得到:
g(x)+x*g(x)=x+2x^2+3x^3+5x^4+8x^5+…
把这最后一个式子和第一个式子好好对比一下。如果第一个式子的系数往左边移动一位,然后把多余的“1”去掉,就变成了最后一个式子了。由于递推函数的性质,我们神奇地得到了:g(x)+x*g(x)=g(x)/x-1。也就是说,g(x)*x^2+g(x)*x-g(x)=-x。把左边的g(x)提出来,我们有:g(x)(x^2+x-1)=-x。于是,我们得