假设你有两份工作供你选择:工作一,有1/2的概率获得1000块钱,有1/2的概率获得2000块钱;工作二,百分之百地能稳拿1500块钱。虽然看上去两种选择的平均收入都一样,但是人们往往更愿意选择后一份工作,尽可能避免前一种工作所带来的风险。为什么面对期望收入相同的事件,人们往往愿意选择风险更小的那一个呢?前几天我去听微观经济学的课时,学到了解释该现象的一个非常有趣的科学模型(经济学大牛请直接无视掉)。
这里,我们有一个重要的假设:收入的边际效用是递减的。换句话说,增加同样多的收入,低收入者主观上会感觉自己收益了很多,本来就是高收入的人则觉得这点儿收入算不了什么。人们往往会觉得,收入从1000块钱增加到2000块钱所带来的幸福感,要远远大于收入从8000块增加到9000块所带来的幸福感。因此,如果把个人收入和它给人带来的效益画成一条曲线的话,大致就如图中的那条蓝色曲线。
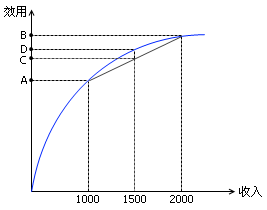
假如你获得了1000元钱,你主观上获得的收益就用A点来表示;假如你获得了2000元,你主观上的收益就在B点。因此,工作一带给你的平均效用就用A和B的中点C来表示。但是,如果我直接就给你1500块钱,你将会得到一个大于C的效用D。这表明,直接选择工作二所带来的效用要高于工作一带给你的平均效用,自然人们都会选择工作二了。因此经济学中有这样一个定理,如果一个人认为自己收入的边际效用是递减的,那么这个人就是一个风险规避者。对于期望收入相同的两件事来说,他愿意去做风险更小的那一件。