Using your Head is Permitted 数学谜题站的主持人 Michael Brand 某日收到了来自 R. Nandakumar 的一个谜题:是否有可能把一个矩形剖分成若干个小矩形,使得每个小矩形的形状互不相同,但它们的面积都一样?没有想到,从这个问题出发,加上一些非常机智巧妙的分析与构造,我们能得到越来越多有意思的东西。于是,它就变成了 Using your Head is Permitted 今年 3 月的谜题。看了谜题的答案后,我也被彻底折服,决定把这一系列的思考重述在此,和大家一同分享。为了简便起见,下面的“矩形剖分方案”一律指的是把一个大矩形分割成若干个小矩形的方案。
几何
正多边形的滚动与旋轮线下方的面积
想像一个圆盘在地面上滚动一周,那么圆周上一点所形成的轨迹就叫做旋轮线(或者摆线)。旋轮线下方的面积是多少,这是一个非常有趣的问题。据说, Galileo 曾经用一种非常流氓的方法,推测出了旋轮线下方的面积。他在金属板上切出一块圆片,再在金属板边缘剪下这个圆形所对应的旋轮线,把它们拿到秤上一称,发现后者的重量正好是前者的三倍。于是,他推测,半径为 r 的滚轮所产生的旋轮线,其下方的面积就是 3πr2 。

不过,今天我第一次知道,这个结论对于正多边形是同样成立的。
趣题:用最少的点挡住所有可能的反射路径
有一个正方形的房间,房间的四壁都是镜子。房间里有一个天使和一个恶魔。假设房间是一个单位正方形 [0, 1] × [0, 1] ,那么天使和恶魔便是这个正方形内的两个点 (a, b) 和 (c, d) 。恶魔想要在原地发射致命激光杀死天使(激光可以无限地在镜子间反射)。天使可以根据恶魔的位置,预先在房间里放置一些守卫为自己挡住激光(守卫实际上也是一个个点)。当然,天使可以在自己周围密密麻麻地放一圈守卫,围成一个封闭的圆形,从而让恶魔不管朝什么方向发射激光,最终都无法击中天使。我们的问题是,能把守卫的数量减少到可数个点吗?能把守卫的数量减少到有限个点吗?
这是一个非常经典的问题,我已经见过不止一次了。它可以重新叙述为很多更有趣的实际问题。去年的这个时候,网友 Spark 发来邮件,分享了他在看台球比赛时想到的一个问题:最少需要摆放多少个球,才能挡住白球到目标球的所有可能的路线,迫使对手犯规?如果我们把台球也抽象成一个一个的点,问题就和前面提到的情况一样了。
今天,我终于看到了这个问题的答案,颇为激动,在此和大家分享。
趣题:舞台里的狮子
有一个半径为 10 米的圆形舞台,初始时舞台上的某个地方有一头狮子。这头狮子在舞台上以折线段的方式跑了 30 千米。求证:在整个过程中,这头狮子至少转了 2998 个弧度。
有时候,换一个角度思考,问题就会迎刃而解。
经典证明:不断把凹的部分翻出来,总能把凹多边形变凸吗?
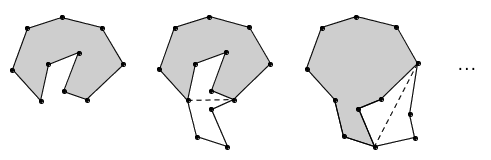
左图是一个凹多边形,而且凹得相当厉害。作为一个完美主义者,我很难容忍这么一个图形,总想着要把凹进去的部分翻出来,把它还原为一个凸多边形。不幸的是,翻折之后的结果仍然不是凸多边形,图中又产生了新的凹陷。于是,我们想继续把凹进去的部分往外翻,直到整个图形变成凸多边形为止。问题是,这个过程有完吗?换句话说,我们一定能通过有限多步翻折,把凹多边形变成凸的吗?
这个问题有着非常纠结复杂的历史。这个问题最早可能是由数学家 Paul Erdős 正式提出的。 1935 年,他在 American Mathematical Monthly 上猜想,经过有限步翻折之后,凹多边形一定能变凸。 1939 年, Béla Szőkefalvi-Nagy 给出了一个证明。因此,这个结论又叫做 Erdős-Nagy 定理。有趣的是,这个问题是如此的自然,以至于在此之后,又有一大堆人重新提出并研究了这个问题,而且他们明显并不知道相互之间的已有研究。这事儿给我们带来的好处就是,我们有了 Erdős-Nagy 定理的好几种截然不同的证明方法。不过,这些证明或者太长,或者太高深,或者又有些漏洞。 1999 年, Godfried Toussaint 从这些证明中取长补短,给出了一个比较初等的证明。