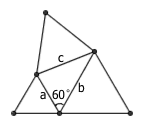
有一个三角形，三边长分别为 a 、 b 、 c ，其中 a 、 b 两条边夹角为 60° 。分别以 a 、 b 、 c 为边向外作等边三角形。求证：前两个等边三角形的面积之和，减去第三个等边三角形的面积，将等于原三角形的面积。
几何
经典证明：Ptolemy定理的无字证明
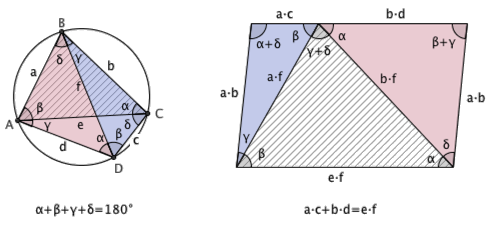
Ptolemy 定理是平面几何中非常漂亮的定理：圆内接四边形的对边乘积之和等于对角线的乘积。具体地说，如果把一个圆内接四边形的四条边顺次记为 a 、 b 、 c 、 d ，把两条对角线的长度记为 e 和 f ，那么一定有 a · c + b · d = e · f 。 Ptolemy 是一个非常重要的定理，由它出发可以得出很多推论。例如，在圆内接矩形上应用 Ptolemy 定理，可以立即得到勾股定理。下面是另外两个可以用 Ptolemy 定理来解决的问题：证明余弦定理，以及构造两两间的距离都是整数的点集。
William Derrick 和 James Hirstein 在最近的 The College Mathematics Journal 上给出了下面这个 Ptolemy 定理的无字证明，你能看明白吗？
难倒犹太人的五个数学问题
这个 Blog 已经不止一次提到过难倒犹太人的“棺材问题”了。很多年以前，要想进入莫斯科国立大学的数学系，你必须通过四项入学考试；头两个都是数学考试，一个笔试，一个面试。在面试中，学生和考官都是一对一的，考官可以自由向学生提出任何他喜欢的问题。考官们都准备了很多“棺材问题”，这些问题的答案非常简单，但由于思路太巧妙了，以至于学生很难想到。考官便可以以“你连这个都没想到”为理由，光明正大地拒绝学校不想要的人（主要是犹太人）。之前我们曾经介绍过一个典型的“棺材问题”：空间四边形外切于给定球，求证四切点共面。去年的这个时候，我们还介绍了同样机智巧妙的 11 个问题。
民间还流传着很多其他的“棺材问题”列表。 Ilan Vardi 曾经写过一篇题为 Mekh-Mat Entrance Examinations Problems 的论文，收集了 25 个“棺材问题”，并给出了解答。这篇论文被收录进了 You Failed Your Math Test, Comrade Einstein 一书中。 Ilan Vardi 发现，这 25 个问题的“难法”有所不同。虽然其中不乏思路奇巧的好题，但也有不少步骤繁琐（当然也有可能是还没找到好的解法）、题意不清甚至结论错误的题目。这里，我选择了其中五个有趣的题目，写下来和大家一同分享。
贴着另一枚硬币旋转一周则自身转了两周：不同的解释方法
有一道非常经典的智力问题：假设有两个一模一样的硬币 A 和硬币 B ，如果让硬币 B 不动，让硬币 A 贴着硬币 B 旋转一周，那么硬币 A 自身旋转了多少周？一个常见的错误答案是“显然也是一周啊”，而实际上正确的答案是两周，如下图所示。我们有很多方法来解释这种现象，其中最传统的说法便是“公转了一周，自转了一周”。硬币 A 的运动是由两部分合成的，公转一周（想像一个人绕着地球走了一圈），以及自转一周（想像一个轮子在地面上滚动了一周）。想像你是站在硬币 B 中心处的一个小人儿，看着硬币 A 贴着你脚下的硬币转动一圈。如果在此过程中，你始终面向硬币 A ，那么在你看来，硬币 A 似乎就是在长为 2πr 的平地上滚了一圈。而实际上，在观察硬币 A 的过程中，你自己也原地转了 360 度，因此从外面的人看来，硬币实际上转了两周。
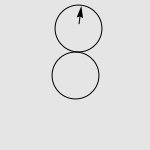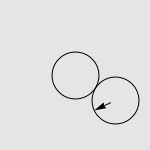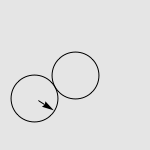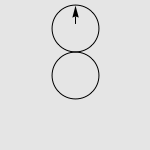
写了这篇文章后，我习惯性地开始用正多边形逼近的思路去分析一些与圆有关的一般性结论。在准备一份初中几何问题的材料时，我突然想到了上述问题的一个简单而漂亮的解释方法。
趣题：构造多边形使得过边界上某一点的任意直线均能等分面积
这是 2008 年莫斯科数学竞赛中的一个问题。构造一个多边形，使得这个多边形的边界上存在这样的一个点 O ：经过点 O 的任意直线均会把该多边形分成面积相等的两部分。这看起来不大可能对吧？但其实构造却并不困难。你能想出来吗？