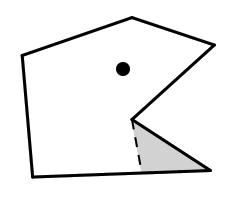
下面是趣题集 Which Way Did the Bicycle Go 中的第 71 个问题。如下图，在这个六边形的围墙中，如果站在图中圆点的位置，那么有两面墙不能被完全看见（其中一面墙完全看不见）。能否设计出一个多边形围墙，使得站在围墙里面的某个地方后，所有的墙都至少有一部分是不可见的？
几何
趣题：斜边上的动点
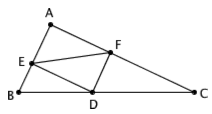
这是一个非常经典的问题。如图，三角形 ABC 是一个直角三角形， ∠A = 90° 。 D 是斜边 BC 上的一个动点。过点 D 作 AB 和 AC 的垂线，垂足分别为 E 和 F 。问题：当 D 点运动到什么位置的时候，线段 EF 最短？
趣题：同时等分三角形周长和面积的直线
求证：对于任意一个三角形，一定存在一条直线，它把这个三角形的周长和面积同时分成了两等分。
大家知道，三角形的三个内角的角平分线一定交于一点，这个点就是三角形的内心，它到三角形三边的距离是相等的。一个令人吃惊的结论是，经过内心的直线如果平分了三角形的面积，就一定平分了三角形的周长！
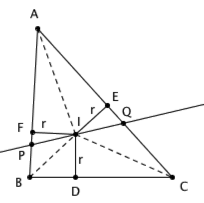
如图， I 是三角形 ABC 的内心， ID 、 IE 、 IF 是 I 到三角形三边的垂线段，它们的长度是相等的，不妨把这个长度值记作 r 。假设直线 PQ 经过点 I ，并且平分三角形的面积。这说明， PA · r / 2 + AQ · r / 2 = PB · r / 2 + BC · r / 2 + CQ · r / 2 ，也就是 PA + AQ = PB + BC + CQ 。因此，直线 PQ 也平分了三角形 ABC 的周长。
趣题：平行线之间的正方形
经典证明：任意三角形都能被分成n≥4个等腰三角形
证明：对于任意一个三角形和任意一个大于等于 4 的正整数 n ，都存在一种把这个三角形分割成 n 个等腰三角形的方案。这个问题曾经出现在 1976 年的 Crux Mathematicorum 上。 1977 年， Gali Salvatore 给出了一个非常漂亮的解答。