下面这个结论是 Andrew Jobbings 在 2011 年指出的：
AB 是圆 O 的一条直径， CD 、 EF 是两条垂直于 AB 的弦，并且以 CD 为直径的半圆和以 EF 为直径的半圆正好切于点 T 。那么，两个半圆的面积之和一定等于圆 O 的面积的一半。
你能证明这个结论吗？
几何
两两接触的等粗且无限长的圆柱体
大家在吃饭喝酒时是否注意到了这样的事情：三个人碰杯时，每个人的杯子都能同时和其他两个人的杯子相接触，很完美；但是四个人碰杯时，任一时刻总会有两个人碰不到杯，非常尴尬。有一次和三个好朋友吃饭，四人碰杯时又发生了这种尴尬的情况，突然有一个人异想天开，把他的杯子放到了另外三个杯子的上面，从而实现了四个杯子两两接触！我们自然引出了这样一个问题：如果 n 个全等的圆柱体两两相接触，则 n 最大是多少？
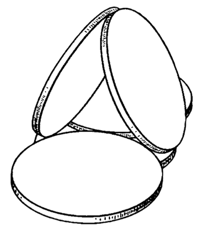
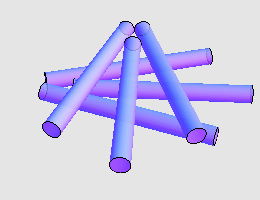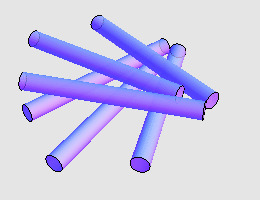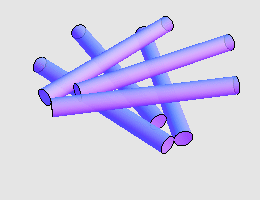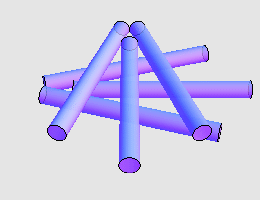
对于不同形状的圆柱体，答案可能是不一样的。 Martin Gardner 在 Hexaflexagons and other mathematical diversions 一书中提到，我们可以精巧地摆放 5 枚硬币，使得它们两两相接触，如上图所示（注意，最底下还藏着一枚硬币）。同时， Martin Gardner 问到，能否摆放 6 支香烟让它们两两接触？一个经典的答案如下：
怎样把一个钝角三角形分成若干个锐角三角形
这是我最喜欢的几何谜题之一：你能否在纸上画一个钝角三角形，然后把它分割成若干个锐角三角形？令人难以置信的是，这竟然是可以办到的！继续看下去之前，大家不妨先自己想一会儿。
每次我在课堂上提出这个问题的时候，学生们总会疯狂而盲目地进行尝试。根据我的观察，绝大多数人都会先画一个不那么钝的钝角三角形（其实这本质上并不会简化我们的问题），然后作出一系列类似于图 1 的尝试，但最后都以失败告终。此时我往往会反复强调：要有方法啊，要有方法！首先，想必很多人已经注意到了，我们必须在钝角里引出一条线（如图 2 所示），这样才能把钝角给消除掉。接下来，则是很少有人意识到的一点：我们不能让这条线一直延伸到对边，否则原三角形将会被分成一个锐角三角形和一个钝角三角形（或者两个直角三角形），这并不能解决根本问题。也就是说，这条线在到达对边前就必须得分岔。最后一个关键的问题就是，分成几岔？显然，分成三岔（如图 3 所示）是不够的，因为这样只能把一个周角分成四份，它们不可能都是锐角。为了让所有的角都是锐角，我们至少要让这条线分成四岔（如图 4 所示）。最后，再把一些没有连起来的点连起来，我们就得到一个像模像样的答案了（如图 5 所示）。
一个与球内接多面体体积有关的问题
在所有周长相等的长方形中，正方形拥有最大的面积；在所有周长相等的平面图形中，圆拥有最大的面积；在所有表面积相等的长方体中，正方体拥有最大的体积；在所有表面积相等的立体图形中，球拥有最大的体积。所有这类问题的答案都是越对称的图形越好吗？ George Pólya 在 Mathematical Discovery 一书中的第 15 章里举了下面这个例子。
在给定圆周上选取四个点构成一个四边形，那么正方形的面积一定是最大的吗？答案是肯定的。只要有哪个点不在相邻两点之间的圆弧的中点处，我们都可以把它移动到这段圆弧的中点处，使得整个图形的面积变得更大。好了，我们现在的问题是，在球面上选取八个点构成一个顶点数为 8 的多面体，那么正方体一定是体积最大的吗？
