假设平面上有 1 + 2 + 3 + … + n 个小球,每个小球的质量都是 1kg 。它们排成了一个三角形阵,具体地说,它们排成了一个倒置的、以 (0, 1) 为顶点的等边三角形。这个三角形阵作为一整个物体,它的重心的 y 坐标是多少?我们有两种不同的求解方法。
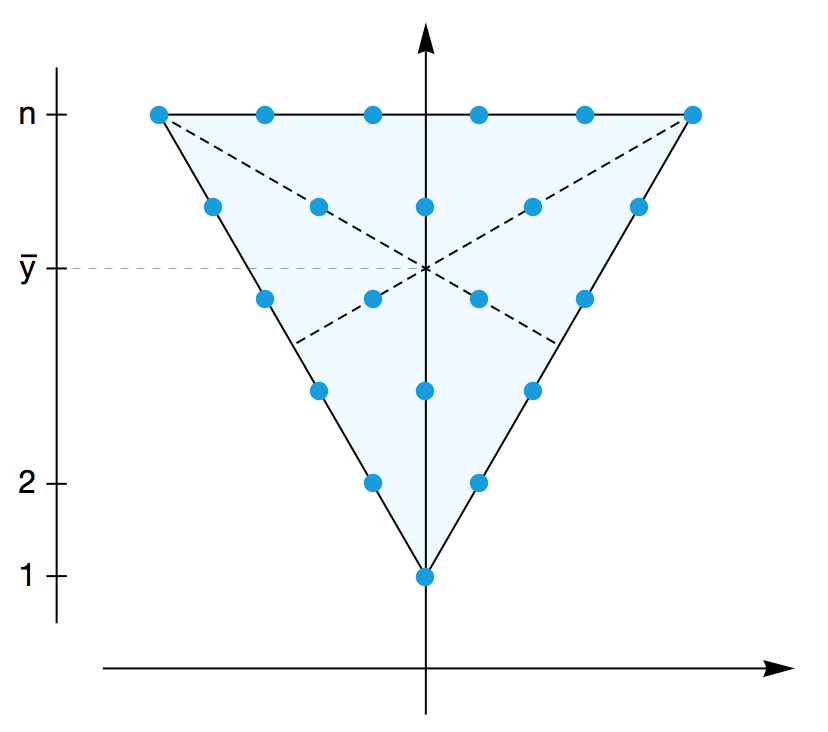
假设平面上有 1 + 2 + 3 + … + n 个小球,每个小球的质量都是 1kg 。它们排成了一个三角形阵,具体地说,它们排成了一个倒置的、以 (0, 1) 为顶点的等边三角形。这个三角形阵作为一整个物体,它的重心的 y 坐标是多少?我们有两种不同的求解方法。

小明和狮子同被关在一个半径为 10 米的竞技场里,狮子位于竞技场的圆心处,小明则在距离圆心 1 米的地方。两者的最大运动速度都是每秒 1 米。狮子有没有什么必胜策略,使得不管小明怎么跑,它总能在有限的时间里抓住小明?
根据 MathWorld 相关词条的描述,这个问题是由 R. Rado 在 1925 年时提出的。一个经典的“答案”是,狮子只需要始终保持自己与小明在圆盘的同一半径上即可。直觉上看,由于狮子总是处在“内圈”上,因而不管小明跑到了哪里,狮子总能轻松地与小明继续保持在同一半径上;并且,狮子总有足够的余力向小明靠近,严格减小它与小明之间的距离,除非小明是沿着半径方向径直向外跑。由于竞技场的大小是有限的,小明不可能无限地向外跑,因而狮子最终总会追上小明。但是,后来人们发现,这个解法其实是错误的,原因很简单:能不断靠近小明,不一定就能在有限的时间里抓住小明,正如 1/2 + 1/4 + 1/8 + 1/16 + … 永远不会超过 1 一样。最终, A. S. Besicovitch 为小明构造出了一个极其巧妙的策略,使得狮子无论如何都抓不到小明,从而完美地解决了这个问题。不过, MathWorld 的词条里并没有提到这个解法。你能想到这个解法吗?
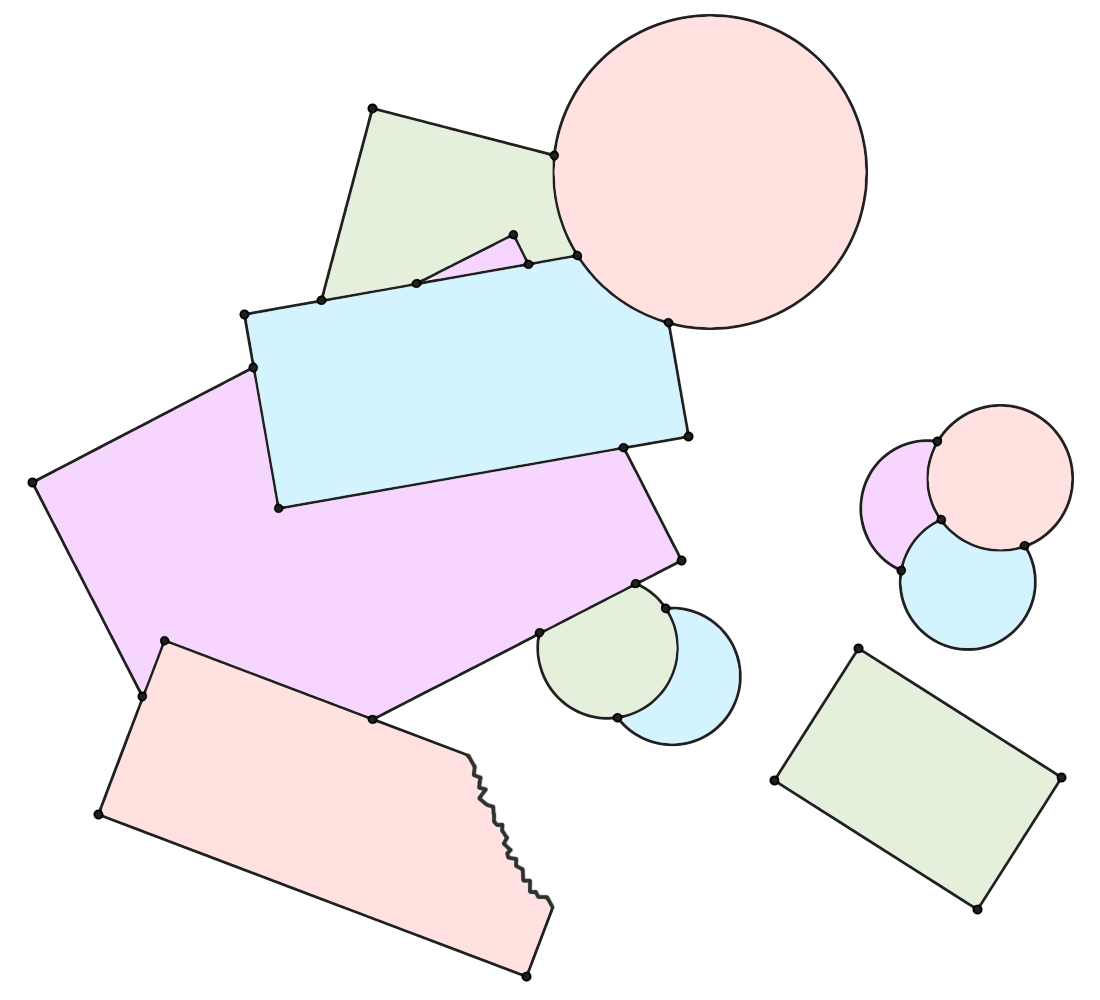
5 张矩形的纸片和 6 张圆形的纸片散落在桌面上,如下图所示(其中一张矩形纸片被撕掉了一个角)。考虑所有露在外面的矩形顶点以及纸张边缘处的交点,你能否从中找出四个保证共圆的点?很简单,右下角那个绿色矩形的四个顶点就满足要求,因为矩形的四个顶点显然是共圆的。其实,在这个图里,还有另外三组满足要求的点,你能找到吗?