射影几何太科学了！太科学了！以后我要慢慢写进Blog里。这里说一个《什么是数学》中射影几何章节中的一个小插曲，和射影几何本身没太大关系：纸上两点A和B，它们之间的距离大于直尺的长度。你如何只用直尺作出过这两点的连线？注意，你只能使用笔和直尺，不能借助圆规等其它工具。
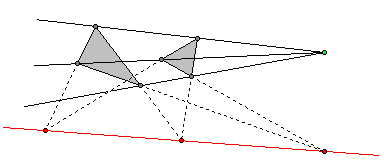
首先让我们回顾一下射影几何中的Desargues定理。Desargues定理描述了一个由简单的点和线所构成的美妙的关系：平面上的两个三角形的对应顶点的连线共点，则对应边的交点共线。你可以多画几个图来验证这一结论，这里不再介绍完整的证明了。另外，虽然题目中的直尺不能连接距离太远的两点，但别忘了直尺可以无限延长一条已有的线段，你只需要不断重复“延长 – 描新点”的步骤就可以了。
上个月Erich Friedman的Math Magic提出了这样的问题：
给定一个指定形状的棋盘，给定一个大于2的整数n，找出一个面积最大的图形S使得n个S能够不重叠地装进这个棋盘里。
问题提出之后得到了不少有趣的构造，这些构造是否为最优解还有待进一步证明。
由三个格子组成的棋盘共有两种本质不同的形状。“长条形”已经不用多考虑，“拐角形”中n=2, 3, 6时的最优解也是非常显然的。拐角形棋盘是可以分成四等分的。但是，在这个棋盘中放置5个相同的图形就没那么容易了。已知的最优方案占据了整个棋盘约0.959的面积。放置7个相同的图形研究起来更困难一些。已知最优解为0.956。
多年以前，要想进入莫斯科国立大学的数学系，你必须通过四项入学考试；头两个都是数学考试，一个笔试，一个面试。在面试中，学生和考官都是一对一的，考官可以自由向学生提出任何他喜欢的问题。那时，为了筛选出他们不想要的应试者（主要是犹太人），很多考官都会出一些题目描述简单有趣、解答过程极其巧妙而又出人意料的问题。这些问题极具杀伤力，民间戏称其为“棺材问题”(coffin problems)。下面这个问题就是其中一个“棺材问题”：
考虑一个空间四边形A1A2A3A4，它的四条边A1A2, A2A3, A3A4, A4A1都与一个给定的球相切。求证，这四个切点共面。
为了更好地理解这个问题，考虑一个菱形的钢架沿对角线折叠，或者一个正四面体钢架去掉相对的两条棱。把这个空间四边形当成一个碗去接一个球，你会发现这个球卡在空间四边形中掉不下去了，此时它与四条边都相切。凭借我们的生活经验，我们很容易提出这个猜想：四个切点是共面的。
上个月IBM Ponder This的题目：给出足够多的正三角形和正四边形（均为单位边长），你需要用它们拼接出凸多边形。注意，你所拼出来的多边形的每条边也必须都是单位长度（因此，把两个正方形拼在一起形成的1*2长方形就不算）。你能拼出多少种不同的凸多边形？在看答案之前，大家先自己想一想，比比看谁考虑得最全面。这对思维的全面性是一个不小的挑战。
首先，注意到符合条件的方案肯定是有限的。由于最终的图形不允许出现平角，因此凸多边形的内角最大也只能到150°。显然，这样的凸多边形面积是有限的，最极端的情况就是一个正12边形（内角均为150°）。
去年的一篇日志里曾经向大家提到了Smale球面外翻问题：在允许与自身相交的情况下，是否有可能无损地、平滑地、不留折痕地把一个球面的内侧翻到外面来。那篇日志里有一个视频，演示了球面外翻的其中一种解法，但没有再进行任何说明和解释。我曾在Google Video上找到了一段完整的视频，可惜Google Video不对中国大陆开放。当时我非常想看一看这段21分钟的视频，但尝试了各种方法都不行，其它地方也没有找到。今天听说中国大陆可以看Google Video的视频了，首先想到的就是去看这段视频。确实太精彩了！！你可以看到球面外翻问题有解的可能性，以及低维情形下（圆的外翻）为何反而无解。后面多个角度多种方式的动画演示足以让你完全理解这个外翻过程中的每个细节。从第11分钟开始的那个add waves则是整个视频的精华所在，太牛B了！
把地址给出来吧，如果上面这个看不了可以进这里面去看：
http://video.google.com/videoplay?docid=-6626464599825291409