下面这个有趣的问题来自IMO 2008第一题,题目给出的结论非常美妙。
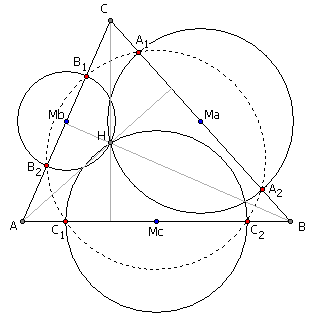
给定一个锐角三角形△ABC,垂心为H。Ma、Mb、Mc分别为三条边的中点。以Ma为圆心,过点H的圆与线段BC相交于点A1、A2;类似地,以Mb、Mc为圆心,过点H的圆与三角形交于B1、B2、C1、C2。求证,A1、A2、B1、B2、C1、C2六点共圆。
几何
七点共圆:一个美妙的结论
L: Change the WorLd中的数学题

电影中涉及数学的地方很少有经得起仔细琢磨的。记得《考试一家亲》中那个小屁孩儿上去背圆周率没背几位就开始乱整了;要想骗骗观众,至少你得查一查前20位的精确值吧。这些细节很多电影都忽视掉了,就连电影pi开头的圆周率都是错的。
但在L: Change the WorLd里,几处涉及数学的地方都经得起推敲。估计大家应该还记得那个数字方阵式的密码吧?我们亲眼目睹到了这一密码的破译过程:写成一串,两位两位隔开,按字母表顺序转换为对应的字母,按题目(的另一种理解方式)去掉HOPE四个字母,最后得到WATARI(就是渡的名字)。
另一处扯到数学的地方是那个答案为MK的几何题。这个题不是瞎编的,做出来的答案真的就和片中的一样,连最后那个小屁孩儿在黑板上画的辅助线都是正确的。
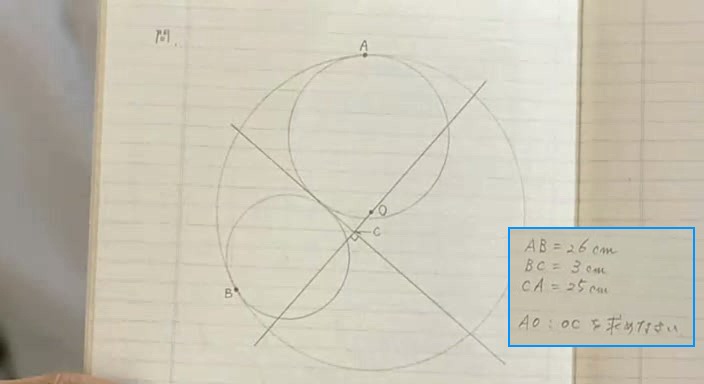
如果AB=26,BC=3,CA=25,请问AO:OC是多少?
视频推荐:Dimensions – A walk through mathematics
刚在sdyy那儿看到了这个好东西。影片Dimensions长约2个小时,共分为9章,谈论了维度、射影、复数等有趣的数学话题。下面是一个4分钟长的预告片。完整的视频可以在这里下载。
经典证明:Cantor-Bernstein-Schroeder定理
明天考英语,单词还没背。先冒死更新一个^_^
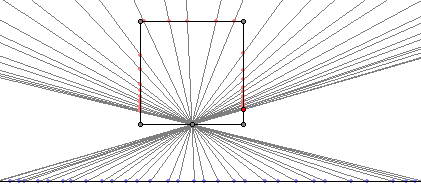
我们称一个从集合A到集合B的映射是“单射”的,如果A中的任两个相异元素都不会映射到B里的同一个元素。如果一个A→B的映射是单射的,并且B里的所有元素都被射了(满射),那么这个映射就是“双射”的。Cantor-Bernstein-Schroeder定理是说,假如存在一个从集合A到集合B的单射函数f,以及一个从集合B到集合A的单射函数g,那么A与B之间一定存在一个双射函数(即能建立起一一对应的关系,两个集合有相等的势)。这个结论并不是显然的。对于无穷集合,我们可以构造出很多这样的例子,两个映射A→B和B→A都是单射,但都不是满射的。例如,给定一个正方形和正方形外的一条直线,把正方形放到直线上滚一圈所形成的对应关系是一个从正方形上的所有点到直线上的点的一个单射函数,而连接直线上的点和正方形一边中点后与正方形的另一个交点构成了一个从直线到正方形的单射关系(如图)。那么,根据Cantor-Bernstein-Schroeder定理,我们一定可以找到一种函数,使得直线上的所有点和正方形上的所有点有一一对应的关系。