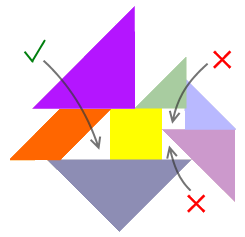
有时候，我们需要一个不用倒带即可实现无限循环播放的特殊磁带。这并不是不可能，只需要打开磁带外壳，把基带进行适当的剪切粘贴后重新绕上去即可。上图便是一个简单的循环播放磁带设计图，磁带的基带非常短，只能录制大约4.9秒。可循环播放的磁带与传统磁带不同的就是，如果基带是一个“圈”的话，它无法再在转轴上一圈一圈地缠绕，否则将会产生自相交，而这在卡带中是不允许的。在这种情况下，基带不可能设计得太长，任何一个小小的改动，哪怕是从4.9秒提升到5秒，也是一个不小的胜利。
下图是另一种设计方案，录制时间从4.9秒一下子提升到了7.8秒。
有网友可能敏锐地发现，这个设计似乎有问题——两个转轴的旋转方向不一致。事实上，在卡带中，转轴的转动方向不一致是允许的。显然，卡带的两个转轴中只能有一个是主动旋转，另一个则是被动旋转；这是因为在播放普通卡带时，由于两个转轴各自最外圈的基带半径不同，两个转轴的转速是不一样的，播放卡带必然只能是用一轴带动另一轴。
现在，我们的问题是，有一种循环播放磁带设计方案，可以将录制时间增加到9.3秒。你能想到这个方法吗？
概率论并不仅仅是用来算算概率的。有些时候，概率论远比我们想象中的更强大。
考虑这样一个问题。考虑集合X上的一个集合族，集合族中的所有集合大小均为d。我们说这个集合族是可以二染色的，如果对X的元素进行适当的红蓝二着色之后，每个集合里面都包含了两种颜色的元素。例如，当d=3时，{1,2,3}, {1,2,4}, {1,3,4}, {2,3,5}就是可二染色的，把1、2染成红色，把3、4、5染成蓝色，则每个集合里都含有两种颜色。是否存在d=3的不可二染色集族呢？这样的集族当然是存在的，例如取集合{1,2,3,4,5}的全部C(5,3)个元素个数为3的子集，则无论如何染色，总会有一个集合里面的元素全是一种颜色。上述推理立即告诉我们，对于一个给定的d，一定存在一个集合个数为C(2d-1, d)的不可二染色集族。这个数目还能再少吗？我们想知道，不可二染色集族中的集合个数最少可以少到什么地步。一个极其简单的证明给出了一个下界：集族的大小一定大于2^(d-1)。当d=3时，你一辈子也不能构造一个不可二染色集族，里面只含4个集合。
为了证明这一点，不妨对X中的所有元素进行随机着色，每个元素取成红色和蓝色的概率均等。那么，一个元素个数为d的集合中，所有元素均为一种颜色的概率就应该是1/2^(d-1)。如果集族内的集合个数只有不到2^(d-1)个，那么即使“集合中是否只有一种颜色”是互相独立的，这些事件的并（至少有一个集合内只有一种颜色）的概率也不超过2^(d-1) * 1/2^(d-1) = 1，何况这些事件还不是独立的，因此存在单色集合的概率必然小于1。这个概率值小于1说明什么？这说明，“至少有一个单色集合”并不是必然事件，一定有一种染色方案使得每个元素里都含两种颜色，换句话说该集族可以被二染色。
我为最新一期的《博物》杂志写了一篇关于七巧板的文章。文章中我提到了一个有趣的问题：一副七巧板拼出的图形里最多可以有多少个中空的“洞”？Martin Gardner认为，一块副七巧板最多能拼出有三个洞的图形，并且他自己给出了一个非常漂亮的构造。如果你手中有七巧板的话，不妨也来试试看；没有七巧板也不必觉得遗憾，网上遍地都是七巧板Flash游戏。觉得困难的话，不妨先从两个洞开始做起。
注意，一个中空的洞必须完全被七巧板的内部空间所包围，仅仅是端点相触由七巧板边界围成的洞是不算的。因此下面的图形中其实只有一个洞，另外两个都不符合规范。
Klein瓶是拓扑学中最神奇的几何体之一，以至于谁家里要是有一个Klein瓶的话我愿意花500块钱把它买下来。不过呢，瞻仰不到Klein瓶也没关系，不要忘记Geek始终是一种富有创造力、喜欢自娱自乐的生物。做不出玻璃瓶子不要紧，做一个“山寨Klein瓶”可谓是出奇的简单。你只需要截取长袖T恤的两条袖子，在其中一个的表面上打一个洞，让另外一个袖子穿过去，然后把对应的口子缝起来即可。然后呢，以后无聊时你就又多了一件事情可以干了：把这个玩意儿拿出来，不停地、没完没了地把“里面”翻出来。
