在机器时代，作为机械构造的理论工具，连杆系统曾一度成为数学界中最热门的话题。所谓连杆系统，就是一些刚性的小杆在端点处以转轴的方式相连，形成的一个机械装置。固定某些顶点的位置之后，其余的动点就能画出一些有趣的轨迹。比方说，固定线段 AB 的其中一个端点 A ，则顶点 B 将描绘出一个绕 A 点的圆周。
连杆系统最激动人心的，莫过于一些简单的连杆装置能够描绘出非常复杂的曲线。例如，上面的右图就是由五根相同长度的线段构成的连杆。固定 A 、 B 两个端点后，显然 C 和 D 描绘出的都是圆弧，但 E 点的轨迹就很难以想象了。事实上， E 点的轨迹相当的诡异，需要用一些复杂的代数语言才能描述。
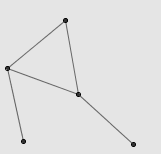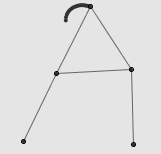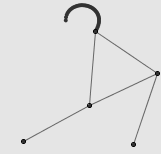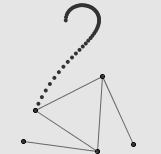
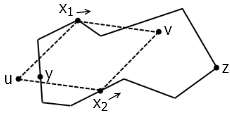
这一系列文章的最后，我们将证明：任意凸多边形内均存在内接正方形。事实上，这几乎是“任意凸多边形内均存在内接菱形”这一命题的直接推论。在这篇日志中，我们实际上证明了这样一个结论：在任意凸多边形中，任选一个方向 u ，总能找到一个内接菱形，它的其中一条对角线与所选方向平行。
现在，慢慢旋转方向 u ，则所得菱形的两条对角线将连续地变化。当方向 u 旋转了 90 度后，原来的两条对角线交换了位置，换句话说两条对角线的长度之差变号了。因此，在方向 u 旋转的过程中，必然有一个时刻两条对角线的长度恰好相同，此时内接正方形也就得到了。
可能有的读者想问了，去掉“凸多边形”这一条件，任意多边形内都存在内接正方形吗？答案是肯定的。 Square Peg 定理告诉我们，对于任意一个简单多边形，总能在上面找到四个点，使得它们恰好是一个正方形的四个顶点。定理的证明需要用到很多之前提到的类似的方法，不过更加复杂一些，这里就不再叙述了。
最后还有一个有趣的话题想与大家分享一下。大家看到了，在一个多边形内内接等边三角形、矩形、菱形甚至正方形都是没有问题的，那么这类问题的极限在哪里？有什么图形是一个多边形内不能内接的吗？肯定是有的。下面我们证明，存在一个多边形，它不能内接正七边形。
事实上，任何三角形内都不能内接正七边形。考虑一个正七边形的外接圆，它与三角形最多只有六个交点（因为一条线段和一个圆最多只能产生两个交点），因此正七边形显然是不能内接于三角形内的。
我们曾经用两种巧妙的方法证明了这样一个命题：任意凸多边形内均存在内接菱形。利用上次讲到的登山引理，我们可以证明一个更强的命题：任意多边形内均存在内接菱形。
证明的大致思路如下：在多边形外任选一点 u 。把多边形上离 u 最近的点记作 y ，把多边形上离 u 最远的点记作 z 。 y 和 z 这两个点就把整个多边形的边界分成了两个部分。
你相信吗，仅仅利用一张日落的照片，你就能得出地球的半径大小！ Princeton 大学的 Robert Vanderbei 在最近的一篇论文中对一张摄于密歇根湖的日落照片进行了分析，不但证实了地球是圆的，还依据照片上的内容对地球半径进行了估算。我把计算的大致过程向大家描述一下，供大家膜拜。
事情的起因就是上面这张很平常的日落照片，以及这样一个大家平时并没有太在意的问题：太阳露出水面的部分应该是一个标准的弓形，但为什么在日出日落时，我们所看到的太阳是一个橄榄球一样的形状？大家或许会很快想到，发光体的下半部分其实是日光反射在水面上造成的。随之产生的是另一个问题：为什么它的下半部分要比上半部分小一些呢？
23. 一些硬币互不重叠地放在桌上。四色定理告诉我们，若要对硬币进行染色，使得挨在一起的硬币颜色不同的话，最多只需要四种颜色就可以了。存在至少需要四种颜色的构造吗？
答案：存在。如图，若只允许三种颜色的话， A 的颜色必须与所有阴影硬币颜色相同， B 的颜色也必须与所有阴影硬币颜色相同， A 、 B 将会同色。
