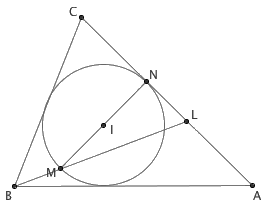
动脑时间咯！搞搞几何题，脑子不生锈。作出任意三角形 ABC 的内切圆 ⊙I ，它与 AC 相切于点 N 。过 N 作 AC 的垂线，与 ⊙I 的另一个交点记作 M （因此 MN 就是这个圆的一条直径）。连接并延长 BM ，与 AC 交于点 L 。求证： CN＝AL 。
几何
谬证大全：1+1≠2的n种可能
最近看到几个有趣的数学谬证，想写下来与大家分享；结果写到这个又想到那个，一写就写个没完，于是想到干脆做一篇谬证大全，收集各种荒谬的证明。
如果你有什么更棒的“证明”，欢迎来信与我分享，我会更新到这篇日志中。我的邮箱是 matrix67 at tom.com ，或者 gs.matrix67 at gmail.com 。
1=2？史上最经典的“证明”
设 a = b ，则 a·b = a^2 ，等号两边同时减去 b^2 就有 a·b – b^2 = a^2 – b^2 。注意，这个等式的左边可以提出一个 b ，右边是一个平方差，于是有 b·(a – b) = (a + b)(a – b) 。约掉 (a – b) 有 b = a + b 。然而 a = b ，因此 b = b + b ，也即 b = 2b 。约掉 b ，得 1 = 2 。
这可能是有史以来最经典的谬证了。 Ted Chiang 在他的短篇科幻小说 Division by Zero 中写到：
There is a well-known “proof” that demonstrates that one equals two. It begins with some definitions: “Let a = 1; let b = 1.” It ends with the conclusion “a = 2a,” that is, one equals two. Hidden inconspicuously in the middle is a division by zero, and at that point the proof has stepped off the brink, making all rules null and void. Permitting division by zero allows one to prove not only that one and two are equal, but that any two numbers at all—real or imaginary, rational or irrational—are equal.
这个证明的问题所在想必大家都已经很清楚了：等号两边是不能同时除以 a – b 的，因为我们假设了 a = b ，也就是说 a – b 是等于 0 的。
趣题：过纸张外的一点作直线
晚饭之后一起来动动脑吧。纸上有两条夹角很小的直线 a 、 b ，它们在纸外交于一点 O 。在纸上还有一点 P ，大致位置如上图所示。请你利用圆规和（没有刻度的）直尺作出一条同时过 O 、 P 的直线。当然，你不能把图作到纸张外面去。
《新知客》趣题专栏 2010.09
目前，我正在《新知客》杂志上主持一个趣题栏目。每月杂志发行后，我将在 Blog 上同步更新。点击 这里 可以查看往期题目。
推理
1. 在每一个小题中，我们都列出了八种物品，其中前面四种物品都有一个共同点，而这个共同点是后面四种物品所不具有的。请您找出这个共同点来。
(1) 小肠、地毯、水蜜桃、贵宾犬 | 牙刷、足球、藤椅、冰块
(2) 电线、棋子、指示灯、扇形图 | 闹钟、绳子、条形码、井字棋
(3) 电池、钥匙、酵母、书签 | 火柴、魔方、药瓶、订书机
2. 小 A 站在甲、乙两地之间的某个位置，他想乘坐出租车到乙地去。他看见一辆空车远远地从甲地驶来，而此时整条路上并没有别人与他争抢空车。我们假定车的行驶速度和人的步行速度都是固定不变的，并且车速大于人速。为了更快地到达目的地，小 A 应该怎样做呢？你认为下面哪种思路是正确的？
(A) 由于车速大于人速，小 A 应该尽可能早地上车，充分利用汽车的速度优势。因此，小 A 应该迎着空车走上去，提前与车相遇。
(B) 为了尽早到达目的地，小 A 应该充分利用时间，马不停蹄地赶往目的地。因此，他应该自己先朝目的地走一段路，再让出租车载他走完剩下的路程。
趣题：半径相等的半圆和圆 内接正方形的面积之比
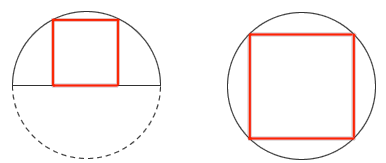
在半径相等的半圆和圆中各画一个内接正方形。这两个正方形的面积之比是多大？有什么简单些的算法吗？
Read more…