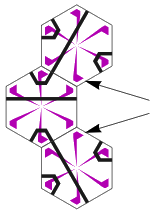
数学教师 Suman Vaze 在业余时间里，把一个个经典的几何定理搬上了画布。不对称的几何图形蕴含了一种更深层的对称性，无疑带来了位于构图和色彩之外的另一种美。这下，似乎又有新的油画派别诞生了——几何定理派。
在平行四边形中，过图形中心的直线将平分整个图形的周长。在上面这个由三个半圆组成的图形中，同样的性质仍然成立。证明的任务就留给大家自己去做了。
几何
最帅的Menelaus定理证明方法
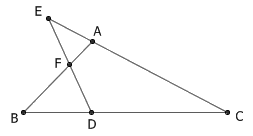
Menelaus 定理是平面几何中用于判断三点共线的一个常用定理。在 △ABC 中，点 D 、 E 、 F 分别在 BC 、 AC 、 AB 所在直线上，若 D 、 E 、 F 三点共线，则有 AF/BF · BD/CD · CE/AE = 1 。 Menelaus 定理的证明方法有很多，今天我见到了我所见过的证明方法中最帅的一种，它解决了之前很多证明方法缺乏对称性的问题，完美展示了几何命题中的对称之美。
神一般的定理，以及神一般的证明
趣题：面积为1的凸多边形总能放进一个面积为2的矩形里
证明：任意给定一个面积为 1 的凸多边形，我们总能把它放进一个面积为 2 的矩形里。
注意，这里“凸多边形”的条件是必需的——如果图形不是凸的，很容易想出反例来。
能平铺平面，却不能周期性地平铺平面
看看自己脚下的地板——虽然正方形、长方形、正六边形等图形都能平铺整个平面，但平铺的方式却非常无聊，不过是同一种模式不断重复罢了。有没有什么“非平凡”的平铺方案呢？下面就给大家看这样一个图形，加上一些限制条件之后，它仍然能够平铺整个平面，不过平铺出来的结果却非常神奇——它并不能通过简单的重复得到，也就是说它不具有周期性。
下图就是这个传说中的地板砖（及其镜像）：
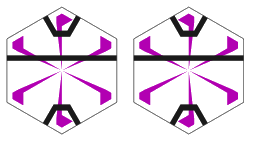
拼接时有两个要求：
(1) 黑色的线条必须连在一起
(2) 一条边两端的紫色小旗必须朝向相同的方向（如箭头所示，注意两个小旗来自于两个不相邻的砖块）
