上图的拍摄者一定是个桌游达人，五种正多面体骰子的全家福竟然都能被他搞出来。我们自然会想到一个有趣的问题：还有别的形状的骰子吗？或者更“数学”一些的说法，在凸多面体的每个面上都标一个数字，能用来当骰子的就只有这五种吗？看上去似乎是这样：只有正多面体才能保证这颗骰子是“公平”的。呃⋯⋯是吗？
几何
集数学与艺术于一体的几何幻方
Lee Sallows 最近做了一个网站，收集了很多在几何意义上也成立的幻方，集数学与艺术于一体，为传统意义的幻方赋予了新的生命。大家来欣赏一下吧。
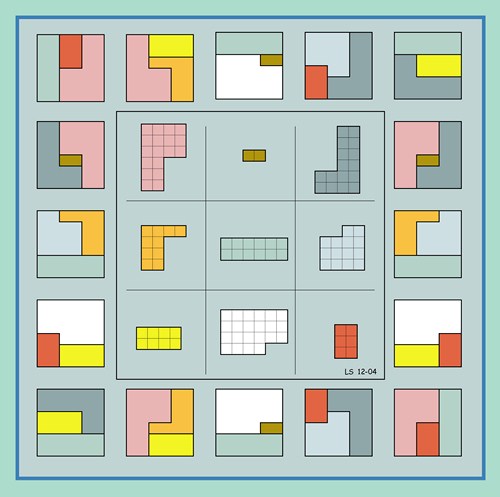
这是一个幻方，它由九块积木组成。这些积木所含的小方格数分别是 2, 6, 8, 10, 12, 14, 16, 18, 22，每行每列和两对角线上的方格总数都是 36 。 牛 B 的是，每条线上的三块积木正好也都能拼成一个 6 × 6 的矩形。
出租车几何学：一个全新的几何世界
从北大打车到四惠，我一定会选择走四环。虽然从北京城中间直穿过去看上去很诱人，但考虑到北京道路几乎总是正南正北的方向，不会真有人认为这样能抄近路吧。在城市中，我们估算两点之间的距离时，往往不会直接去测量两点之间的直线距离，而会去考虑它们相距多少个街区。在理想模型中，假设每条道路都是水平或者竖直的，那么只要你朝着目标走（不故意绕远路），不管你怎样走，花费的路程都是一样的。今天，我看到了一个非常有意思的名词——出租车几何学 (taxicab geometry) ，其名称就来源于这样的想法。
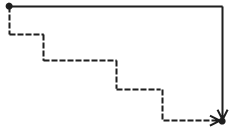
在出租车几何学中，点还是形如 (x, y) 的有序实数对，直线还是满足 a x + b y + c = 0 的所有 (x, y) 组成的图形，角度大小的定义也和原来一样。只是，(x1, y1) 和 (x2, y2) 的距离重新定义为了 |x1 – x2| + |y1 – y2| ，即两点的横坐标之差加上纵坐标之差。
这是一个对“距离”的合理定义，因为它满足
- 非负性：两点距离总是大于等于 0
- 对称性： A 到 B 的距离等于 B 到 A 的距离
- 零距离： A 到 B 的距离为 0 当且仅当 A = B
- 三角形不等式：对于任意三点 A 、 B 、 C ，不等式 AB + BC ≥ AC 总成立
也就是说出租车几何学是建立在一个合理的度量空间上的。这是一个全新的几何世界。
千万别学数学：最折磨人的数学未解之谜（一）
数学之美不但体现在漂亮的结论和精妙的证明上，那些尚未解决的数学问题也有让人神魂颠倒的魅力。和 Goldbach 猜想、 Riemann 假设不同，有些悬而未解的问题趣味性很强，“数学性”非常弱，乍看上去并没有触及深刻的数学理论，似乎是一道可以被瞬间秒杀的数学趣题，让数学爱好者们“不找到一个巧解就不爽”；但令人称奇的是，它们的困难程度却不亚于那些著名的数学猜想，这或许比各个领域中艰深的数学难题更折磨人吧。
作为一本数学趣题集， Mathematical Puzzles 一书中竟把仍未解决的数学趣题单独列为一章，可见这些问题有多么令人着迷。我从这一章里挑选了一些问题，在这里和大家分享一下。这本书是 04 年出版的，书里提到的一些“最新进展”其实已经不是最新的了；不过我也没有仔细考察每个问题当前的进展，因此本文的信息并不保证是 100% 准确的，在此向读者们表示歉意。
这篇文章很长，大家不妨用自己喜欢的方式马克一下，一天读一点。
趣题：两两间的距离都是整数的点集
最多能在平面上找出多少个点，使得它们两两之间的距离都是整数？当然，我们忽略最平凡的解——所有点都在一条直线上。
三个点的解显然是存在的，只需要构造一个边长为 1 的等边三角形即可。事实上，满足任意两数之和大于第三数的一组整数都可以成为一个三角形的三条边。寻找含有四个点的解也并不困难，一个长为 4 宽为 3 的矩形就能满足要求。不过，我们还有更小一些的解。最小的解貌似是下面这个等腰梯形：上底、下底分别是 3 和 4 ，两腰都是 2 ，两条对角线都是 4 ，正好也都是整数。
那么，能否找到平面上的五个不共线的点，使得两两之间的距离都是整数呢？最多能找到多少个这样的点呢？