曾经想过要写一篇科幻小说，讲一种生活在空壳星球内表面的文明，如何发现自己的星球是圆的，如何成功地环游世界一周，又如何发现自己其实是在星球的内表面。今天我长出了一口气，幸好当初没写这样的文章，不然就闹笑话了。今天我才知道，空壳星球内部的人是不能居住在星球的内表面的，因为空壳星球内的任意一点都没有重力。
这其实并不难理解。虽然脚下的土地离你更近，产生的重力作用更显著，但可惜这部分土地并不多。星球的更多部分将会位于你的头上，但可惜它们又离你太远了，影响也不会太大。近的部分太小，大的部分又太远，这两者很可能是一种平衡的状态。
在这个 Blog 的一篇很老很老的文章里，我曾经讲过一个非常有趣的几何作图问题，这个问题最早是由 D. Pedoe 教授在 1983 年提出的：给定 A 、 B 两点，只用一个生锈的圆规（没有直尺），如何找出一个点 C ，使得 A 、 B 、 C 恰好构成一个等边三角形？所谓“生锈的圆规”，也就是一个被卡住的圆规，它的两脚张角不能改变。我们不妨假设，它只能画出单位大小的圆。1987 年，我国的侯晓荣等人成功地解决了这个问题，并借助复平面理论得到了很多一般的结果，其研究成果《锈规作图论》发表在了《中国科学技术大学学报》上。
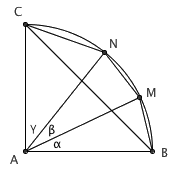
锈规作出等边三角形的方法非常漂亮：利用锈规作图，我们能构造出两点之间由单位长线段构成的折线段，进而实现平行四边形的构造（已知其中三个点，能够只用锈规找出第四个点），进而完成等边三角形的构造。刚才提到的那篇“很老很老的文章”里有详细的描述，继续阅读之前，强烈建议先看一看。
事实上，D. Pedoe 教授还提过另外一个问题：给定 A 、 B 两点，只用锈规能否作出 A 、 B 连线的中点？注意，由于没有直尺，线段 AB 实际上是画不出的。要想“隔空”找出线段的中点，显然并不容易。
前几天翻起张景中的《数学家的眼光》，就是为了查阅这个问题的解决方法。《数学家的眼光》一书中详细描述了锈规作图找中点的方法，在这里和大家分享。
偶然瞥见一道很妙的题目：已知三个锐角 α 、 β 、 γ 的和为 90°，求证：sinα + sinβ + sinγ > 1
这个问题的证明方法有很多，不过大家一定会喜欢下面这个证明：
作一个半径为 1 的 90° 扇形，于是图中 α + β + γ = 90° 。注意到 △ABM 的面积可以写成 (1/2) · AB · AM · sinα = sinα / 2，类似地 △AMN 、 △ANC 的面积分别为 sinβ / 2 和 sinγ / 2 ，但他们的面积之和显然大于 △ABC。于是，sinα / 2 + sinβ / 2 + sinγ / 2 > 1/2，即 sinα + sinβ + sinγ > 1 。
这个问题来源于张景中的《数学家的眼光》。
下面这些文字来源于我在初三数学竞赛课的一份讲义。这节课的主题本是四点共圆，但由此引出了三角形中很多漂亮的性质，让人深感数学之美。在此整理出来，献给所有还在中学读书的读者，以及早已远离中学数学的 80 后。不管大家是否喜爱数学，想必都会被这些奇妙的结论所震撼。
三角形的奇迹首先表现在各个“心”上：三角形内部的每一组有几何意义的线条都交于一点。三条角平分线交于一点，这个点就叫做三角形的“内心”，它是三角形内切圆的圆心；三边的中垂线交于一点，这个点就叫做三角形的“外心”，它是三角形外接圆的圆心；三角形的三条中线也交于一点，这个点叫做三角形的“重心”，因为它真的就是这个三角形的重心。用力学方法可以很快推导出，它位于各中线的三等分点处。这些心将会在本文后面某个出人意料的地方再次出现。
三角形的三条高也不例外——它们也交于一点，这个点就叫做三角形的垂心。
垂心看上去很不起眼，但深入研究后即会冒出很多奇妙的结论。由于两个斜边重合的直角三角形将会产生出共圆的四点，因此画出三角形的三条高后，会出现大量四点共圆的情况，由此将挖掘出一连串漂亮的结论。让我们先来看一个简单而直接的结论：
今天是我第一次听说这个故事。
1933 年，匈牙利数学家 George Szekeres 还只有 22 岁。那时，他常常和朋友们在匈牙利的首都布达佩斯讨论数学。这群人里面还有同样生于匈牙利的数学怪才——Paul Erdős 大神。不过当时，Erdős 只有 20 岁。
在一次数学聚会上，一位叫做 Esther Klein 的美女同学提出了这么一个结论：在平面上随便画五个点（其中任意三点不共线），那么一定有四个点，它们构成一个凸四边形。Szekeres 和 Erdős 等人想了好一会儿，没想到该怎么证明。于是，美女同学得意地宣布了她的证明：这五个点的凸包（覆盖整个点集的最小凸多边形）只可能是五边形、四边形和三角形。前两种情况都已经不用再讨论了，而对于第三种情况，把三角形内的两个点连成一条直线，则三角形的三个顶点中一定有两个顶点在这条直线的同一侧，这四个点便构成了一个凸四边形。
