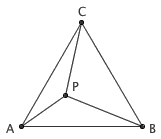
这是初中平面几何的一个经典问题：等边三角形 ABC 内有任意一点 P，求证 PA 、 PB 、 PC 的长度一定能构成一个三角形。
几何
趣题：能否在等边三角形点阵中画一个正方形？
IMO2011趣题：总存在一条将会遍历所有点的直线
下面这个精彩的问题来自于刚刚结束的 IMO 2011 中的第 2 题：
设 S 是平面上包含至少两个点的一个有限点集，其中没有三点在同一条直线上。所谓一个“风车”是指这样一个过程：从经过 S 中单独一点 P 的一条直线 l 开始，以 P 为旋转中心顺时针旋转，直至首次遇到 S 中的另一点，记为点 Q 。接着这条直线以 Q 为新的旋转中心顺时针旋转，直到再次遇到 S 中的某一点，这样的过程无限持续下去。
证明：可以适当选取 S 中的一点 P ，以及过 P 的一条直线 l ，使得由此产生的“风车”将 S 中的每一点都无限多次用作旋转中心。
趣题：不用相似怎么办？
我老早就写过一个经典的小学几何题。如果你还没看过这个问题，你一定要去看看。一个小学奥数老师曾经告诉我，当年带领学生参加这次竞赛时，领队老师们都没有想到这个问题的“小学生解法”，以至于开始质疑这道题是否超纲了。看到答案后，老师们大为折服——这个问题确实有一个无需任何几何知识的妙解。
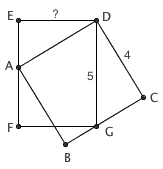
今天，同样的事情发生了。今天临时去代一节小学奥数课，见到这么一道题： ABCD 是一个正方形，边长为 4 ， DEFG 是一个矩形，其中 DG = 5 ，求 DE 的长度。还是那段话：题目本身并不难，大家一看就知道答案；问题的关键在于，这个问题是一道小学竞赛题，这意味着这个题目一定有一个异常巧妙的傻瓜解。这个解法不用相似形，不用列方程，事实上几乎什么都不用，只需要用到最基本最显然的正方形长方形的性质。你能想到这个解法吗？
盯着结论看，直到它变得显然成立为止
很多看上去很显然的结论，其实是需要严格证明的，并且有时候证明相当困难。比方说算术基本定理，每一个数分解质因数的方法都是唯一的。这看上去几乎是显然的，但证明过程需要很多深刻的数论知识。更极端的例子则是 Jordan 曲线定理，即平面上每一条不与自身相交的封闭曲线都把平面分成了里外两部分。这几乎就是一句废话，但要想严格证明起来相当不容易， Camille Jordan 本人的证明最后发现竟然也是错误的。
最近 MathOverflow 上有人提了一个非常有趣的问题：有那么多结论很显然但证明很困难的定理，那有没有什么结论很不可思议但证明过程却不言而喻的定理呢？
在众人的回答中，呼声最高的就是 Desargues 定理：若三角形 ABC 和 A’B’C’ 中， AA’ 、 BB’ 、 CC’ 所在直线交于一点，则两个三角形中每一组对应边的交点（即 BC 和 B’C’ 的交点 D 、 AC 和 A’C’ 的交点 E 、 AB 和 A’B’ 的交点 F ）是共线的。
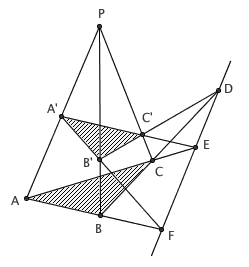
这个定理看上去太神奇了，大家一定会以为证明很难吧。但事实上，这个定理根本不需要证明，它显然是成立的。现在，把 P-ABC 看成一个三棱锥，而 A’B’C’ 则是一个不平行于底面的截面。由于 AB 、 A’B’ 在同一平面内，因此这两条线会相交；这个交点既在平面 ABC 上，也在平面 A’B’C’ 上，因而也就在两平面的交线上。同理，另外两个交点也都在平面 ABC 和 A’B’C’ 的交线上，因此三个交点共线。当然，画在纸上的也好，照相机照出来的也好，人眼看到的也好，其实都是一个二维图形罢了。因此，命题在平面上也是成立的（这背后的逻辑是，在立体图形的平面投影中，直线仍然是直的，共线的仍然共线，共点的仍然共点；借助射影几何的思想，我们能给出一个更严格的证明）。
这个证明神就神在，当你悟到之后，整个证明过程不但不需要一个字，而且连图形说明都可以不用，只需要盯着原图看，结论自己就跳出来了。看来，我们又多了一种证明问题的思路：盯着问题看，直到它突然一下变得显然成立了为止。