Heron 公式是一个已知三角形三边长便能直接求出其面积的经典公式。把三角形的三边长分别记作 a 、 b 、 c ,令三角形的半周长 p = (a + b + c) / 2 ,则三角形的面积可以用 Heron 公式 S = √p(p – a)(p – b)(p – c) 求出。如果把 p = (a + b + c) / 2 代入式子,得到的公式其实也挺对称的: S = √(a + b + c)(a + b – c)(a – b + c)(- a + b + c) / 4 。
现在,我们把这个公式看作是一个关于 c 的函数: f(c) = √(a + b + c)(a + b – c)(a – b + c)(- a + b + c) / 4 。它的导数是多少?
注意到,利用平方差公式,根号内的式子可以进一步整理为 ((a + b)2 – c2)(c2 – (a – b)2) ,它的导数是 – 2c(c2 – (a – b)2) + 2c((a + b)2 – c2) = 4c(a2 + b2 – c2) 。因而,整个原函数的导数就是 c(a2 + b2 – c2) / (2 · √(a + b + c)(a + b – c)(a – b + c)(- a + b + c) ) 。
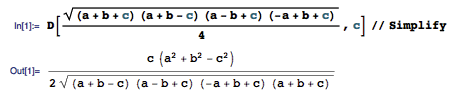
有趣的是,当 a 、 b 、 c 满足勾股定理的关系 a2 + b2 = c2 时,导数值正好为 0 。这是为什么? Heron 公式的导数的零点和勾股定理有什么联系呢?