代码

牛B的Mathematica：寻找开头和结尾都是字母y的形容词

/ 647 条评论

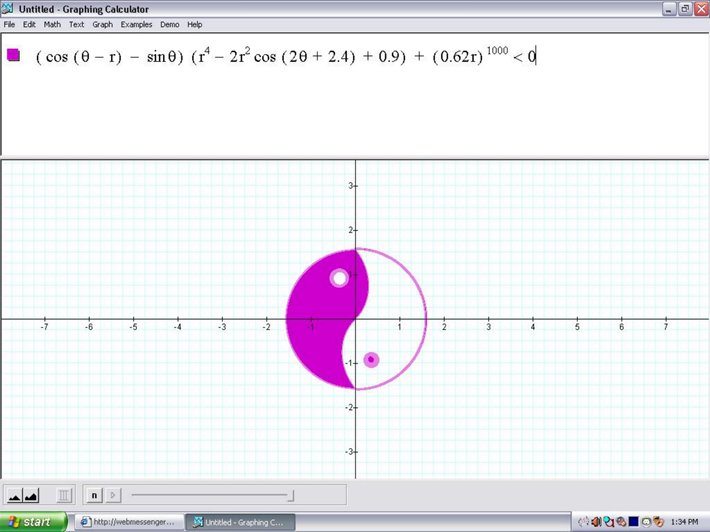
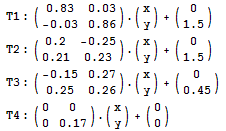    只有想不到，没有做不到。还是在这里，我惊奇地发现Mathematica居然有DictionaryLookup和WordData这样的函数（我的6.0里就有，不知道5.x有没有）。于是，一连串牛B的Mathematica用法出现了：

 
包含ijk三个连续字母的单词：
In[1]:= DictionaryLookup["*" ~~ "ijk" ~~ "*"]
Out[1]= {"Dijkstra"}

 
连续三次出现重复字母的单词：
In[2]:= DictionaryLookup[RegularExpression[".*(.)1(.)2(.)3.*"]]
Out[2]= {"bookkeeper", "bookkeepers", "bookkeeping"}

 
首尾三个（及以上）的字母完全相同的单词：
In[3]:= DictionaryLookup[RegularExpression["([a-z]{3,})[a-z]*1"]]
Out[3]= {"abracadabra", "anticoagulant", "antidepressant",
"antioxidant", "antiperspirant", "bedaubed", "beriberi", "bonbon",
"cancan", "chichi", "couscous", "dumdum", "entailment",
"entanglement", "entertainment", "enthrallment", "enthronement",
"enticement", "entitlement", "entombment", "entrainment",
"entrancement", "entrapment", "entrenchment", "froufrou", "hotshot",
"hotshots", "ingesting", "ingoing", "ingraining", "ingratiating",
"ingrowing", "ionization", "mesdames", "microcosmic", "murmur",
"muumuu", "outshout", "outshouts", "physiography", "pompom",
"redelivered", "rediscovered", "respires", "restores",
"restructures", "tartar", "tessellates", "testates", "testes",
"tormentor", "tsetse", "underfund", "underground"}

Read more…

Ubigraph：强大而易用的图论动画生成软件

/ 13 条评论

    Ubigraph是一个全新的图论动画生成软件，利用它你可以快速生成图论模型的图形和动画，直观地展示出各种图论模型的三维结构，演示各种图论算法的过程，非常适合用于研究和教学。之前本Blog曾经介绍过一个类似的软件graphviz，但这里提到的Ubigraph显然更强大一些。上面的动画就是由Ubigraph生成的二叉查找树演示动画（高清版here），看上去相当的酷。值得一提的是，Ubigraph也是相当易用的。graphviz有它自己的语法规则，而Ubigraph则直接支持Python, Ruby, PHP, Java, C, C++等几乎所有主流语言，因此不管你原先使用的是什么语言，你都可以很快地融入到Ubigraph来。例如，在C语言中包含一个头文件UbigraphAPI.h，你便可以像往常一样用循环语句“画”一个环。

#include <UbigraphAPI.h>
 
int main(int const argc, const char ** const argv)
{
int i;
for (i=0; i < 10; ++i) ubigraph_new_vertex_w_id(i);   for (i=0; i < 10; ++i) ubigraph_new_edge(i, (i+1)%10);   sleep(2);   ubigraph_clear(); }

    你可以在这里下载这个软件。目前该软件暂时没有Windows版。

牛！Mathematica还能这样用！自己制作马赛克拼图

/ 52 条评论

    Wolfram的Blog上更新了一段非常牛的Mathematica代码，真的让我大开眼界。只需要三行代码，你就可以自己做一个马赛克拼图。
imagePool = Map[With[{i = Import[#]}, {i, Mean[Flatten[N[i[[1, 1]]], 1]]}] &, FileNames["Pool/*.jpg"]];
closeMatch[c_] := RandomChoice[Take[SortBy[imagePool, Norm[c - #[[2]]] &], 20]][[1]];
Grid[Reverse[Map[closeMatch, Import["MasterImage.tif"][[1, 1]], {2}]], Spacings -> {0, 0}]

    其中，”Pool/*.jpg”是你的图库，我估计最少也得有几百张吧。我用Photoshop把我的collection全部处理成了35×35的小图；为了让最终效果更佳，我特地把它们全部处理成单色的，并且减小了对比度。”MasterImage.tif”是你的目标图片，Mathematica会把这个图片中的每一个像素用图库中一个合适的图来代替。我把我的照片剪裁了一下，然后压成19×22的大小。Mathematica首先把所有照片以及每个照片的RGB值的中位数存成一个list，函数closeMatch将图片按照RGB值的均方根排序，然后随机从头20个中选出一个。第三行用Grid函数输出我们所要的马赛克拼图。最后我们就得到了——由众MM图所组成的Matrix67的肖像画！！如果你还看不出来的话，站远点儿眯着眼睛就能看出来了。

Read more…

矩阵、随机化与分形图形

/ 30 条评论

    Stetson大学的一个非常可爱的MM（以后本Blog将简称她为Stetson MM）和我分享了一个很神奇的东西。她们正在做一个线性代数的课题研究，题目的大致意思是“用矩阵来构造分形图形”。Stetson MM叫我试着做下面这个实验：对于一个坐标点(x,y)，定义下面4个矩阵变换：
    
    然后，初始时令(x,y)等于(0,0)，按照 T1 – 85%, T2 – 6%, T3 – 8%, T4 – 1% 的概率，随机选择一个变换对该点进行操作，生成的点就是新的(x,y)；把它画在图上后，再重复刚才的操作，并一直这样做下去。我心里觉得奇怪，这为什么会得到分形图形呢？于是我写了一个简单的Mathematica程序：
list = {{0, 0}};
last = {{0}, {0}};
For[i = 0, i < 50000, i++, r = Random[];    If[r < 0.85, last = {{0.83, 0.03}, {-0.03, 0.86}}.last + {{0}, {1.5}},      If[r < 0.91, last = {{0.2, -0.25}, {0.21, 0.23}}.last + {{0}, {1.5}},        If[r < 0.99, last = {{-0.15, 0.27}, {0.25, 0.26}}.last + {{0}, {0.45}},          last = {{0, 0}, {0, 0.17}}.last + {{0}, {0}}        ]      ]    ];    list = Append[list, First[Transpose[last]]]; ] ListPlot[list, PlotStyle -> PointSize[0.002]]

    程序运行的结果真的是令我大吃一惊：竟然真的是一个分形图形！！我不禁再次对数学产生了一种崇敬和畏惧感！！

   

Read more…