堆，就是一陀一陀的东西。头重脚轻不算堆，要上面小下面大才算一个堆。堆是一棵二叉树，满足下面的始终比上面的大。它和二叉查找树比较起来既有好的又有不好的：好的就是要想知道数据里的最小值时根本就不用找了，直接就是最顶上的那个了；不好的就是堆除了这个以外基本上不能做别的事了。除了最顶上的那个以外，你几乎没办法控制其余的部分。当然，插入和删除数据这种基本操作还是可以做的。插入就是把数据暂时先放在最下面的某个位置，然后通过与它上面一个进行比较、交换不断往上冒直到已经到了自己的位置不能再向上为止。删除反起来，通过不断交换往下沉一直沉到底。因为是往下走，所以要考虑到一个把左边的放上来还是把右边的放上来的问题。当然，为了保证堆上小下大的性质，应该把小的一边换上来。刚才说过，由于你只能“看”到最顶上的东西，不知道中间部分是什么样，我们通常只删除最小的（最上面的）那个节点。其实堆还有一个最大的好处：容易写代码。因为我们可以有意让数据把树“排得满满的”，满到它是一行一行挨着排下来的。这叫做“完全二叉树”。我们可以给完全二叉树编个号，从上到下从左到右挨着数下来。根是1，找左儿子就乘2，找右儿子就乘2加1，找它爸就 div 2。以后叫谁就是谁，很方便。这样整个树就可以用一个数组实现了。由于堆基本上只用来找最小，因此如果某个问题要求很复杂的话，最好还是用成二叉查找树；当然，如果问题只要求插入、删除和找最小三种操作，你应该毫不犹豫地选择堆，毕竟找最小时堆方便得多，写起又简单。什么时候出现这种问题呢？比如说，我的女友排起队的，我每次要选一个最纯洁的，就是受那些的影响最小的人。每当我遇见了一个新的美女，我就把她放在这个队伍里合适的位置供我以后娱乐。这时，我只关心每次插入、取最小和删最小。这个队伍就可以用一个堆来优化。因此，堆还有一个形象的名字叫优先队列。如果谁问题目要求不找最小找最大怎么办，那人肯定是个傻子，把堆变通一下，上大下小不就完了吗？

    研究堆麻烦的地方就是堆的合并。如何把两个堆合并成一个堆？这个解决了很有用，至少上面的这些操作跟着全部统一了：插入就是与一个单节点的堆合并，删除根就是把根不要了，把根的左右两边（显然还是堆）合并起来。一个简单的办法就是递归地不断把根大的堆往根小的堆的右边合并，把新得到的堆替换原来的右儿子。注意递归过程中哪个根大哪个根小是不停在改变的。这样下来的结果就是典型的“右倾错误”，而且破坏了完全二叉树的完美。为此，我们想要随时保证堆的最右边尽量少。于是，干脆不要完全二叉树了，不过是多写几行代码嘛。这个不存在像二叉查找树那样“某一边越做越多”的退化问题，因为对于一个堆来说，反正我只管最顶上的东西，下面平不平衡无所谓，只要不挡我合并的道就行。于是，我们想到人为下一个能让堆尽量往左边斜的规定。这个规定就是，对于左右两个儿子来说，左边那个离它下面最近的两个儿子不全（有可能一个都没有）的节点的距离比右边那个的远。这规定看着麻烦，其实还真有效，最右边的路径的长比想像中的变得短得多。这就叫左式堆（左偏树）。这下合并倒是方便了，但合并着合并着要不了多少次右边又多了。解决的办法就是想办法随时保持左式堆的性质。办法很简单，你合并不是递归的吗？每次递归一层后再看看左右两边儿子离它下面没有两个儿子的节点哪个远，如果右边变远了就把左边右边调一下。由于我们已经没有用数组实现这玩意了，因此链表搞起很简单。这个对调左右的方法给了我们一个启发：哪里还要管什么到没有两个儿子的节点的距离嘛，既然我每次都在往右合并，我为什么不每次合并之后都把它对调到左边去呢？这种想法是可行的，事实上它还有一个另外的名字，叫斜堆。

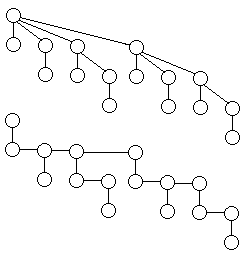
    二项堆更强，它也是堆，也能合并，不过它已经超越了堆的境界了：它不是一个堆，而是满屋子的堆。也就是说，找最小值不能再一下子找到了，而是要把二项堆中的每个堆的顶部都看一下。二项堆的合并也很强，直接把根大的堆放在根小的堆的下面。这意味着二项堆的每个堆都可能不是二叉树了。这增加了编程的难度，不过可以用一个叫做“左儿子右兄弟”的技巧来解决问题。这个技巧，说穿了就是仍然用二叉树来表示多叉树：把树画好，然后规定节点的左儿子是下一层的最左边那个，右儿子就是它右边那个。就是说，左儿子才是真正的儿子，右儿子不过是一起生出来的。为了让二项堆好看些，让堆的个数和大小保持在一个能快速操作的数目和比例内，二项堆作出了一个明智的规定：每个堆的大小（总的节点个数）只能是1、2、4、8、16…中的一个，且每种大小的堆只能有一个。若干个互不相同的2的幂足以表示任意一个正整数，因此这个规定可以保证不管多大的二项堆都能表示出来。保持这个性质很简单，遇到两个大小相等的堆就合并起来成为一个大一号的堆。由于总是两个大小相等的堆在合并，因此二项堆中的每一个堆都有一个奇妙的样子，看看本文结束后下面附的一个大小为16的堆的示意图，再看一下，再看一下，你就能体会到了。图下面有一个用“左儿子右兄弟”法表示的同样的树，其中，往下走的线是左儿子，往右走的线是右儿子。

    最后简单说一下Fibonacci堆。保持一个跟着变的数组记录现在某个节点在堆中的位置，我们还是可以对堆里的数据进行一些操作的，至少像删除、改变数值等操作是完全可以的。但这个也需要耗费一些时间。Fibonacci堆相当开放，比二项堆更开放，它可以不花任何时间减少（只能是减少）某个节点的值。它是这样想的：你二项堆都可以养一屋子的堆，我为什么不行呢？于是，它懒得把减小了的节点一点一点地浮上去，而是直接就把它作为根拿出来当成一个新的堆。每次我要查最小值时我就再像二项堆一样（但不要求堆的大小了）一个个合并起来还原成一个堆。当然，这样的做法是有适用范围的，就是前面说的数值只能是减少。在什么时候需要一个数值只减少不增加的堆结构呢？莫过于Dijkstra一类的图论算法了。所以说，这些图论算法用Fibonacci堆优化可以进一步提速。

Matrix67原创
做人要厚道 转帖请注明出处

    4月7日买起来看，前几天才看完。这可以说明很多问题，比如，学习很紧张，没有时间；书本身很好，很有看头；看书看得很细心，很有耐心。
    打算大致写一下书里的内容。
    Data Structures and Algorithm Analysis in C, Second Edition，机械工业出版社。封面很丑，一个黑底版，上面有些大理石花纹，正中间生硬的摆一个原版封面，同样丑。一共12章，近400页。
    400多页是很多的。我们必须要“把厚书读薄”，厚的变薄的，薄的变一页，一页变一行，一行变成一个字。因此，我要在有限的字数内把整本书说完。

    算法分析，就是复杂度的问题。复杂度只算“最要命的”，比如，执行n^2的算法前来个快排根本不拖速度，n^2多的都豁出去了不在乎区区一个nlogn。书里对复杂度进行了严格的定义，包括O()、o()、Θ()、Ω()四种符号。简单地说，O(n^2)就是顶破天了搞个n^2次；o(n^2)就是天花板不到n^2，比n^2矮一点（比如希尔排序就是o(n^2)，因为它再倒霉也达不到n^2）；Ω(n^2)就是说某个算法随便怎么至少都要耗费n^2，比如所有基于比较的排序都是Ω(nlogn)；Θ(n^2)就是说它即是O(n^2)又是Ω(n^2)，被天花板和水泥地夹在中间了，动不了了，就是它了。这里面有一个经典的例子，就是最大子序列（找数列中连续一段数之和最大）的四种算法，复杂度分别为O(n^3)、O(n^2)、O(nlogn)和O (n)。这书一个特色在于，对每种数据结构都有严格的算法复杂度证明，这往往是看上去最头痛的部分。

    表、栈和队列是三个基本的数据结构。说穿了表就是把数据找起来排排坐吃果果，找什么东西都来把整个队伍找一遍。栈就是一个桶，后放进去的先拿出来，它下面本来有的东西要等它出来之后才能出来，就好像你看到了一个丑人不可能今天的中饭还没吐出来就先把早饭吐出来了。栈是拿来模拟多个过程的调用的（比如递归），实际点的用途就是表达式计算。队列好比堵车，先进去的先出来。先进队先买票，不能插队。常拿来实现广搜。

    树，是一种植物，有很多枝枝丫丫。不同的是这里的树是倒着的，树枝朝下长。最上面叫根，尖尖的地方叫树叶，生出树叶的是他爸，他爸生的是他儿子。不管是根是树叶还是儿子还是儿子他爸都叫节点。我们常常把数据储存在节点上，并且以后还要不断地插入、改变和删除数据。
    二叉树就是每个分叉的地方最多分两个岔，而且还分得清左右。二叉查找树就是说把数据存在节点上，而且左边的都比他爸小，右边的都比他爸大，以后要找哪个数就可以只找其中的一边，一半一半地扔掉。在二叉查找树里也可以插入一个数，删掉一个数（只有一个儿子好办，有两个就把右边的最小的一个拿来替代这个），找最小的数（一直往左走），找最大的数（一直往右走），但是容易搞着搞着的树就变畸形了，比如说左边猛起长右边萎缩导致以后往左边走要走很久。我们就需要一种方法来让树左右差不多一样多而且左边的值仍然比右边的小。事实上这种方法已经找到了，而且不只一种方法，而是一卡车的方法，比如AVL、Splay、红黑树、Treap等。几种方法都靠一个叫“旋转”的技巧，就是把几个节点怎么个一转，左边的就跑到右边去了一点。看下面这个图你就明白了。

         ①                   ②
        /        旋转       /  
      ②   ZZ    ——>    XX  ①
     /                        /  
    XX  YY                    YY  ZZ

这样一来左边就少了，如果左边的XX本来很多的话就可以往上提一层从而平衡。同样地，右边多了反过来做就是了。这只是最简单的“单旋转”，事实上还有很多其它的较复杂的旋转方法。Splay树就是把刚才访问过的节点转啊转啊转啊转转到最顶上去，Treap就是每个节点附加一个随机的数，随时通过旋转保持儿子的这些随机数比他爸大，其余的有点复杂。这些方法都能使二叉查找树相对地平衡一些，防止畸变导致的时间浪费。
    B-树和二叉查找树有两个不同，一个是节点不存数据，数据全在树叶子上，二个是它不一定是二叉。数据仍然左边小右边大方便查找。每个节点最多的儿子数有限制，最多三叉的叫2-3树，最多四叉的叫2-3-4树。因为只有树叶上有数据，所以可以递归地用分裂的方法处理新插入后出现的分叉比规定的最多的儿子个数时还多的情况。比如，2-3树中如果哪里分了四个岔，就把它重新分成两个两个的岔。我们还规定，除了根以外，每个节点最少的儿子数是规定的最多儿子数的一半，除不尽取上整。容易想到，删除的话可以把插入时的分裂反过来做，什么时候只剩一个儿子了就和旁边的合并起来。

    Hash表又叫散列表，一般用于判断有没有重复。比如我想找我们班有没有两个一天生的，我们不必每两个人都来比较一次，而是准备一个年历，让人一个一个上去在他的生日那天那里画一个圈，如果谁要画圈时发现那里已经有一个圈了，就找到了一对。这个很简单，不说了。
    那天班上流行一个心里测试，当时我还真发现了一个和我一天生的，女的。

Matrix67原创
做人要厚道 转帖请注明出处