最近在reddit上看到了这么一个有趣的问题：下图是一个单位立方体，黑色实线分别是立方体相邻两个面的两条对角线。你觉得这两条对角线之间的最短距离是多少？
可以提前告诉你，答案不是√2/2。
趣题
按照盒子的三边长之和来计费有没有漏洞？
这是一个非常有趣的问题。许多快递公司都依据物件的长、宽、高三边之和来收费，一些航空公司也要求托运行李的三边长相加不能超过某个限制。那么是否有人想过，有没有可能把一个三边之和较大的盒子装进一个三边之和较小的盒子里，从而骗取更低的费用呢？有人会说，恐怕不行吧，长宽高之和更大的盒子体积不也应该更大一些吗？不见得。比方说，盒子A的长宽高分别是10、10、10，盒子B的长宽高分别是9、9、12.1。盒子B的三边长之和显然比盒子A要大，但体积只有980.1，比前者要小近20个单位。那么，为什么就不能把盒子B沿斜线方向塞进盒子A呢？有人会敏锐地发现，在上面的例子中，盒子A的体对角线长为17.3205，但盒子B的对角线长度达到17.5616，显然无法完全放进盒子A里。不过且慢，我也能举出这样的例子，三边和更大的盒子其体积和对角线都比小的盒子的要小。盒子A的长宽高分别为10、10、20，盒子B的长宽高分别为7.1、16.5、16.5。盒子B的长宽高之和比盒子A大，体积为1932.98，对角线长度比前者小大约0.1。看来，为了解决这个问题，我们还需要从一些更巧妙的方面入手。
最近几天碰到的几个有趣的问题
最近几天见到了几道零散的、不成系统的趣题，在这里合成一篇文章，与大家分享。
1. 证明：对任意正整数n，n^2+n+1一定不是完全平方数。
2. 说一个实数是可表达的，当且仅当它能用有限长的语句明确地描述出来，如2147483648可以说成是“二的三十一次方”，√2即为“平方后等于二的正实数”，π即为“圆的周长和直径之比”。问题是，是否存在一个不可表达的实数？
3. 一个人有两个小孩儿，其中有一个生于星期二的男孩儿。问另一个是男孩儿的概率是多少？
4. 无需积分，计算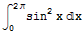
。
趣题：构造骰子使其与两个标准骰子等价
今天下午在上语言统计分析课时，我听到了一个非常有趣的问题。考虑同时抛掷两个骰子所得到的结果——它们的和有1/36的概率得到2，有2/36的概率得到3，……，有1/36的概率得到12。现在，你能否构造两个新的骰子，使得同时抛掷两个新骰子的结果与原来相同？注意，每个骰子都有6个面，每个面都有一个正整数。这些点数可能超过6，并且可能会有重复。另外，这两个骰子也无需完全相同。
解决这个问题并不难。首先注意到，为了使得两个骰子的点数之和能够得达到2，每个骰子上都得有一个“1”（并且仅有一个“1”）才行。接下来考虑，为了得到两种和为3点的情况，我们还得在两个骰子上放置两个“2”：我们可以在每个骰子上各放一个“2”，不过这样就与原来的骰子没啥区别了；我们也可以来点不一样的，把两个“2”都放在一个骰子上。现在，其中一个骰子上只放了一个“1”，另外一个骰子已经填了一个“1”和两个“2”，这可以保证它们能产生出一个2点和两个3点。再下一步，我们将考虑如何产生出三个4点。为此，我们需要把三个“3”分配到两个骰子中。这样推下去虽然越来越麻烦，但最终你还是能得到一个合法解：一个骰子上写有1、2、2、3、3、4，另一个骰子上写有1、3、4、5、6、8。不过，这个问题有一个异常巧妙的解法，它能够把两个骰子的点数进行整体求解。你能想到这个做法吗？
经典证明：一组凸集中任三个的交非空，则所有凸集的交非空
今天看到一本巨爽的电子书，里面介绍了很多离散几何的神奇结论和美妙证明。我一口气看了将近十个小节，期间不停地被那些天才的数学证明所震撼。电子书的第一节介绍了一个非常初等的东西——Helly定理。从这里大家足以领略到凸集理论的奇妙。
Helly定理是说，如果一组凸图形中任意三个都有公共区域，那么所有这些凸图形也一定有一个公共区域。注意，这个结论并不是显然的。如果把“任意三个”改为“任意两个”的话结论就不成立了，反例很容易找。另外，“凸图形”这个条件也是必需的——下图中的四块区域满足任意三个都有交集，但它们却没有一块公共的部分。因此，要想证明这个结论，我们必须充分利用“凸图形”这一条件。
