发现一个有很多智力题的网页,绝大多数题目我都见过,这个Blog之前也曾经介绍过。但是有一个特别有趣的问题让我眼前一亮,之前从来没有见过这类问题。不知道各位网友是否有见过。和大家分享一下。
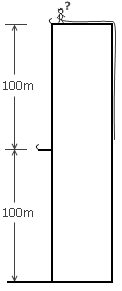
你被困在一幢200米高的大楼的楼顶。你手里有一根150米长的绳子和一把瑞士军刀。你所站的地方有一个铁钩子。往楼下看时,你发现大楼正中间,也就是100米高的位置上,有一个可以落脚的金属支架,上面还有另外一个钩子。你怎样才能利用这些东西安全到达地面?
趣题
算法问题征解:怎样生成随机数而不借助任何工具?
如果你身上没有任何可以使用的工具(手机、mp3、手表、尺子、纸和笔等等),也无法寻求别人的帮助,碰巧这时你突然急需获取一个小于10的随机自然数,你该怎么办?
先抛砖引玉,说说我自己想到的一些办法:
- 取当前年月日之和的个位数(理论上随机性不佳)
- 憋住呼吸并循环慢念0到9这十个数,在吸下一口气之前看念到多少(潜意识会导致随机性不佳)
- 拔10根头发,看第几根最长(可以边拔边比并不断更新最大值)
- 回忆一下看有多少天没来那个了,取个位数(只适用于女性)
- 看身上一共有多少块钱,取个位数
- 完整地唱完一首歌,取歌词字数的个位数
- 随意想一个英文单词,算出所有字母的ASCII码之和并模10
你还能想到哪些有趣的算法?欢迎在下面留言讨论,我会把有意思的留言在这里更新出来。
趣题:某个经典结论的妙用
空间中有六个点,它们两两间的距离都互不相等。考虑所有以这些点为顶点构成的三角形。证明:存在某个三角形,它的最长边是另外某个三角形中的最短边。
这个结论并不是显然的。为了说明这一点,只需要注意到同样的结论对n=5的情况是不成立的。考虑平面上一个正五边形的五个顶点(微调它们的位置使得两两间的距离互不相等),容易发现任意三个点所组成的三角形,其最长边都不可能是另一个三角形的最短边。
趣题:货架上的听装可乐

有一个放听装可乐的货架,它的宽度要比四听可乐的直径稍微大一些。把10听可乐放进这个货架里,堆叠成一个三角形。虽然底下三层可乐罐歪歪斜斜有高有低,但最顶上的那听可乐一定位于货架的正中心,也就是说它到货架两壁的距离是相等的。这是为什么呢?
为什么f'(x)与f(x)/x的交点恰为后者的极值点?
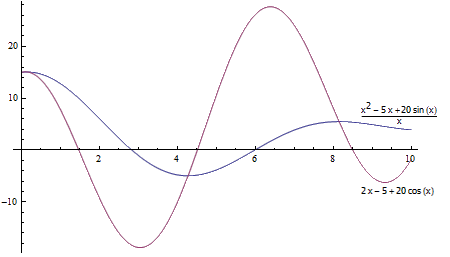
在今天晚上的微观经济学课上,我又听到了一个比较有意思的东西。试着找找各种类型的连续函数f(x),画出f'(x)和f(x)/x的函数图像,你会发现一个奇怪的现象:f'(x)与f(x)/x相交的地方都是f(x)/x取到极值的地方。简单地算一算,我们不难证实这个结论。f(x)/x的导数等于f'(x)/x – f(x)/x^2。将f'(x)=f(x)/x代入上式,可得f'(x)/x – f(x)/x^2 = f(x)/x^2 – f(x)/x^2 = 0。这就是说,当f'(x)与f(x)/x相等的时候,f(x)/x的导数一定等于0。有意思的是,这个结论还有一个非常直观的解释,你能想到吗?