这是一个经典智力问题,不知道大家见过没。下图是一辆自行车在泥地中驶过留下的痕迹,你能据此判断出这辆自行车是从左往右行驶的还是从右往左行驶的吗?
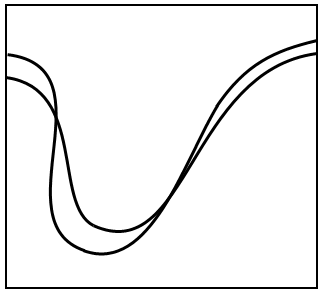
提示:题目条件是充分的,根据这两道车轮印我们足以判定车行方向。这和图中的线条粗细、边缘锯齿没有关系,你完全可以把两道痕迹当作没有粗细之分的理想曲线;为了解决这个问题,必须仔细分析自行车驶过后两道车轮印一定会满足的几何性质。
这是一个经典智力问题,不知道大家见过没。下图是一辆自行车在泥地中驶过留下的痕迹,你能据此判断出这辆自行车是从左往右行驶的还是从右往左行驶的吗?

提示:题目条件是充分的,根据这两道车轮印我们足以判定车行方向。这和图中的线条粗细、边缘锯齿没有关系,你完全可以把两道痕迹当作没有粗细之分的理想曲线;为了解决这个问题,必须仔细分析自行车驶过后两道车轮印一定会满足的几何性质。
IBM Ponder This 上个月的题目很有意思:利用各种数学函数和数学符号,用两个数字 2 得到一个 5 。不过,有一些限制条件:
1. 只能够使用两次数字 2 。因此,像 2 + 2 + 2/2 这样的算式是不行的。
2. 不允许使用变量,因此 (2x + 2x + x)/x 也是不合法的。
3. 不允许使用其它常量,因此 2 + 2 + ln(e) 是不合法的,因为用到了常量 e 。诸如 (2+i)(2-i) 的妙解也因此被禁止了。
4. 不允许使用取整类的函数,否则问题就太简单了,例如⌈√(2*2)!⌉。
说有一个潜水艇,初始时位于数轴上的某个整数点,并沿着数轴以每秒整数个单位的速度做匀速运动(但你不知道具体的初始位置和移动速度是多少,移动方向也是未知的)。每一秒你都可以在某个整数点投放深水炸弹,如果此时潜艇正好在你放炸弹的位置,这个潜艇就被炸掉了。你是否有办法可以保证炸毁潜艇?
这是可以办到的。不管初始时潜水艇在哪儿,它的速度有多大,我总能在有限的时间里炸毁潜艇。假设潜艇的速度为 a ,初始位置为 b ,则在第 t 秒时它的位置就在 a*t + b 。把所有可能的有序数对 (a,b) 看作是平面直角坐标系上的整格点,每次考虑其中的一个点;假设第 i 秒考虑的点是 (a_i, b_i) ,那就在 a_i * i + b_i 处放一个炸弹。如此重复做下去,每次排除一种情况,直到击中目标为止。现在的问题就是,用怎样的顺序遍历平面上的所有格点才能保证每个 (a,b) 都会在有限的时间里访问到。这个方法就多了,比如从原点开始以一条螺旋线为路径一圈一圈地遍历周围越来越远的点。
这个问题展示了一些典型的数学思维在传统智力题方面的应用,它背后的数学方法非常深刻。
来源:http://www.reddit.com/r/math/comments/as2d5/sinking_the_submarine_a_puzzle/
UyHiP上个月的题目:把所有大于 1 的自然数划分成两个集合,证明至少能在其中一个集合里找到互不相同的三个数 a 、 b 、 c 满足 a^b=c 。然后,试着给出一种划分,使得只有其中一个集合里存在这样的三元组。
Update: 后一个问题要求两个集合都是无限集。感谢网友 Triple.J 的提醒。
证明:如果集合 A 里只有有限个数,那就在集合 B 里选两个比集合 A 中的最大数还大的数 a 和 b ,显然 a^b 也在集合 B 里。类似的,若集合 B 里只有有限个数,我们立即可知 A 中存在满足 a^b=c 的三元组。因此,我们只需要讨论两个集合里都有无穷多个数的情况。
从集合 A 里选一个数 x ,从集合 B 里选一个数 y 。无妨假设 xy 在集合 A 中。在集合 A 中选一个比 xy 大的数 r 。由于集合 A 是无限大的,因此这样的数总存在。由于 r 比 xy 大,因此 x 、 y 、 xy 、 r 、 r^x 、 r^(xy) 这六个数两两不同。为了避免在同一集合里出现满足要求的三元组, r^x 和 r^(xy) 都必须在集合B里面,但这样的话, r^x 、 y 和 r^(xy) 就成了符合要求的三元组了。
后一个问题则出奇的简单:把所有素数放进一个集合,所有合数放进另一个集合。显然,一个素数不可能是另一个素数的整数次幂
。
这个月的题目非常有意思,点击这里围观。
今天考完美国结构语言学,稍微轻松了一些。我把前几天向大家推荐的网页好好看了一遍,挑选了10个比较精彩的、不是很常见的、本Blog之前没有提过的智力题,并且把它们都整理到了一起,与大家一同分享。希望大家能够大呼过瘾~
1. 给一个瞎子52张扑克牌,并告诉他里面恰好有10张牌是正面朝上的。要求这个瞎子把牌分成两堆,使得每堆牌里正面朝上的牌的张数一样多。瞎子应该怎么做?
答案:把扑克牌分成两堆,一堆10张,一堆42张。然后,把小的那一堆里的所有牌全部翻过来。
2. 如何用一枚硬币等概率地产生一个1到3之间的随机整数?如果这枚硬币是不公正的呢?
答案:如果是公正的硬币,则投掷两次,“正反”为1,“反正”为2,“正正”为3,“反反”重来。
如果是不公正的硬币,注意到出现“正反”和“反正”的概率一样,因此令“正反反正”、“反正正反”、“正反正反”分别为1、2、3,其余情况重来。另一种更妙的办法是,投掷三次硬币,“正反反”为1,“反正反”为2,“反反正”为3,其余情况重来。
3. 30枚面值不全相同的硬币摆成一排,甲、乙两个人轮流选择这排硬币的其中一端,并取走最外边的那枚硬币。如果你先取硬币,能保证得到的钱不会比对手少吗?
答案:先取者可以让自己总是取奇数位置上的硬币或者总是取偶数位置上的硬币。数一数是奇数位置上的面值总和多还是偶数位置上的面值总和多,然后总是取这些位置上的硬币就可以了。