我找到了这道经典智力题的出处。它似乎来源于一本叫做 Which Way Did the Bicycle Go 的书。这本书又是一本超赞的趣题集，里面有很多我没有见过的趣题妙解。我找到了这本书的电子版，并且传到了自己网站上，与大家分享一下。大家可以点击这里下载。阅读器可以在这里找到。
我整理出了个人认为比较精彩的题目。如果你没有时间翻遍整本书的话，看看我精选出的这些题目也是一个不错的选择。
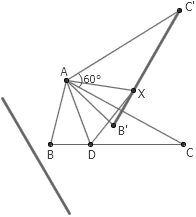
1. 给定 △ABC ，对于平面上的任意一点 X ，它属于点集 S 当且仅当线段 BC 上存在一点 D 使得 △ADX 是等边三角形。点集 S 是什么样子的？
答案：两条线段，它由线段 BC 绕 A 点顺时针或逆时针旋转 60 度而得。这是因为，给定 A 点和 X 点，则 D 点的位置可以由 X 点绕 A 旋转 60 度得到的。既然 D 点在 BC 上，那么显然 X 点就应该在 BC 绕 A 旋转 60 度得到的线段上。
书架的某一层里放了一套百科全书，但它们排列的顺序却是乱的。一个傻子想要把这套书排好顺序，也就是说他想要书架里的书从左至右分别是第 1 卷，第 2 卷，……，第 n 卷。他给这套书排序的办法是这样的：不断取出一本原应放在更左边的书，插进它该在的位置。比方说，某本书的卷号是 3 ，它的位置却是左起第 5 ，位于其目标位置的右侧。那么傻子就可以把这本书拿出来，插入当前左起第 2 本书的右边，把那些占了它位置的书挤到更右边去，而不管这一操作是否会破坏掉已经就位的书。注意到这种排序法很可能捡了芝麻，丢了西瓜，为了一本书的位置而破坏掉一连串原已排好的书，可谓是鼠目寸光，缺乏远见。我们的问题是，在哪些情况下这样的排序法最终一定能实现排序，哪些情况下可能会陷入永无止境的死循环？
显然，过 Pizza 的圆心作四条直线，把一个周角平分成八等份，则整个 Pizza 饼也被分成了八等份。我们也很容易联想到，如果过圆心外的一点做出四条直线，并且同样满足每两条相邻直线夹 45 度角，那么这八块 Pizza 饼显然是不一样大的。考验你直觉的时候到了：你认为蓝色面积之和与红色面积之和相比，哪个大一些呢？
如图，两条直线相交于点 O 。 △ABC 的顶点 A 在其中一条直线上，顶点 B 在另一条直线上。如果保持 △ABC 的各边边长不变，让点 A 和点 B 在所在直线上滑动，那么点 C 描绘出来的轨迹是一个什么样的图形？
在处理最优化问题时，我们常常通过分析导函数来寻找极值点，因此往往希望目标函数是可导的；但在很多实际问题中，目标函数里经常带有取最大值函数，它的存在将破坏函数的可导性。一个有趣的问题由此产生：能否设计一个平滑的二元函数 f(x,y) ，它的效果近似于 max(x,y) ，足以用来代替最大值函数？在设计这样的函数时，下面这些条件需要尽可能满足：
· 函数简洁而美观
· 可以调整函数的“平滑度”
· 可以很方便地扩展到多个变量
