这是一个非常有趣的问题：能否在一个无限大的等边三角形点阵中选取四个点，使得这四个点恰好构成一个正方形？这个问题有一个非常简单巧妙的解法，你能想到吗？
趣题
IMO2011趣题：总存在一条将会遍历所有点的直线
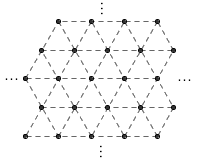
下面这个精彩的问题来自于刚刚结束的 IMO 2011 中的第 2 题：
设 S 是平面上包含至少两个点的一个有限点集，其中没有三点在同一条直线上。所谓一个“风车”是指这样一个过程：从经过 S 中单独一点 P 的一条直线 l 开始，以 P 为旋转中心顺时针旋转，直至首次遇到 S 中的另一点，记为点 Q 。接着这条直线以 Q 为新的旋转中心顺时针旋转，直到再次遇到 S 中的某一点，这样的过程无限持续下去。
证明：可以适当选取 S 中的一点 P ，以及过 P 的一条直线 l ，使得由此产生的“风车”将 S 中的每一点都无限多次用作旋转中心。
趣题：不用相似怎么办？
我老早就写过一个经典的小学几何题。如果你还没看过这个问题，你一定要去看看。一个小学奥数老师曾经告诉我，当年带领学生参加这次竞赛时，领队老师们都没有想到这个问题的“小学生解法”，以至于开始质疑这道题是否超纲了。看到答案后，老师们大为折服——这个问题确实有一个无需任何几何知识的妙解。
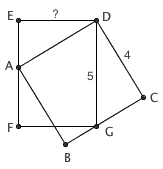
今天，同样的事情发生了。今天临时去代一节小学奥数课，见到这么一道题： ABCD 是一个正方形，边长为 4 ， DEFG 是一个矩形，其中 DG = 5 ，求 DE 的长度。还是那段话：题目本身并不难，大家一看就知道答案；问题的关键在于，这个问题是一道小学竞赛题，这意味着这个题目一定有一个异常巧妙的傻瓜解。这个解法不用相似形，不用列方程，事实上几乎什么都不用，只需要用到最基本最显然的正方形长方形的性质。你能想到这个解法吗？
趣题：连接多个数字串时怎样避免歧义？
今天碰上一个非常有意思的问题。有一条通信线路，每次可以发送一个由数字 0 到 9 组成的任意长的数字串。怎样巧妙地利用这条通信线路，构造一种一次能够发送两个数字串的协议？注意到，直接将两个数字串相连是不行的，因为这将会产生歧义。如果对方收到的数字串是 1234 ，他没法知道你发送的是数字串 12 和 34 ，还是数字串 123 和 4 ，抑或是 1 和 234。
能否把第一个串的位数编码进去，比如把 12 和 34 编码成 21234 ，这样不就知道第一个数字串到哪儿截止了吗？不行，因为你不知道这个位数信息本身到哪儿截止，假如编码结果是 123456789012345 ，你就不知道第一个数字串是 1 位还是 12 位了。换一个思路，能否用几个非常特殊的数字当作分隔符呢？也不行，因为你要发送的数字串里有可能偏偏也包含了这几位数。怎么办呢？
锈规作图续篇：单用一个只能画单位圆的圆规如何作线段中点
在这个 Blog 的一篇很老很老的文章里，我曾经讲过一个非常有趣的几何作图问题，这个问题最早是由 D. Pedoe 教授在 1983 年提出的：给定 A 、 B 两点，只用一个生锈的圆规（没有直尺），如何找出一个点 C ，使得 A 、 B 、 C 恰好构成一个等边三角形？所谓“生锈的圆规”，也就是一个被卡住的圆规，它的两脚张角不能改变。我们不妨假设，它只能画出单位大小的圆。1987 年，我国的侯晓荣等人成功地解决了这个问题，并借助复平面理论得到了很多一般的结果，其研究成果《锈规作图论》发表在了《中国科学技术大学学报》上。
锈规作出等边三角形的方法非常漂亮：利用锈规作图，我们能构造出两点之间由单位长线段构成的折线段，进而实现平行四边形的构造（已知其中三个点，能够只用锈规找出第四个点），进而完成等边三角形的构造。刚才提到的那篇“很老很老的文章”里有详细的描述，继续阅读之前，强烈建议先看一看。
事实上，D. Pedoe 教授还提过另外一个问题：给定 A 、 B 两点，只用锈规能否作出 A 、 B 连线的中点？注意，由于没有直尺，线段 AB 实际上是画不出的。要想“隔空”找出线段的中点，显然并不容易。
前几天翻起张景中的《数学家的眼光》，就是为了查阅这个问题的解决方法。《数学家的眼光》一书中详细描述了锈规作图找中点的方法，在这里和大家分享。